Google
Câu hỏi: Đặt điện áp $u={{U}_{0}}\cos (\omega t+\varphi )$ (U0, ω và φ không đổi) vào hai đầu đoạn mạch AB mắc nối tiếp theo thứ tự cuộn dây thuần cảm có độ tự cảm L, dụng cụ X và tụ điện có điện dung C. Gọi M là điểm nối giữa cuộn dây và X, N là điểm nối giữa X và tụ điện. Biết $\omega {{~}^{2}}LC=3$ và ${{u}_{AN}}=160\sqrt{2}\cos \left( \omega t+\dfrac{\pi }{2} \right)$ (V), ${{u}_{MB}}=40\sqrt{2}\cos \omega t$ (V). Điện áp hiệu dụng giữa hai đầu đoạn mạch MN gần giá trị nào nhất sau đây?
A. 100 V.
B. 71 V.
C. 48 V.
D. 35 V.
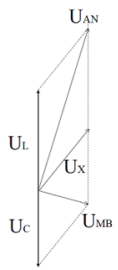
Ta có: ${{\omega }^{2}}LC=3\Rightarrow \dfrac{{{Z}_{L}}}{{{Z}_{C}}}=3$
$\Rightarrow {{U}_{L}}=3{{U}_{C}}$ (1)
Ta có ${{u}_{AN}}$ sớm pha hơn ${{u}_{MB}}$ : $\dfrac{\pi }{2}$
Do đó ta có: ${{U}_{L}}+{{U}_{C}}=\sqrt{U_{AN}^{2}+U_{MB}^{2}}=40\sqrt{17}$ (V)(2)
Từ (1) và (2) $\Rightarrow {{U}_{L}}=30\sqrt{17}\text{ (V); }{{\text{U}}_{C}}=10\sqrt{17}\text{ (V)}$
Ta có: $U_{x}^{2}=U_{AN}^{2}+U_{L}^{2}-2{{U}_{AN}}{{U}_{L}}\cos \varphi $
$\Rightarrow U_{x}^{2}=U_{AN}^{2}+U_{L}^{2}-2{{U}_{AN}}{{U}_{L}}\dfrac{{{U}_{AN}}}{{{U}_{L}}+{{U}_{C}}}$
Với ${{U}_{AN}}=160\ V;{{\text{U}}_{MB}}=40\ V$.
$\Rightarrow U_{x}^{2}=50\ (V)$
Suy ra điện áp hiệu dụng giữa hai đầu đoạn mạch MN gần giá trị 48V nhất
A. 100 V.
B. 71 V.
C. 48 V.
D. 35 V.
Ta có: ${{\omega }^{2}}LC=3\Rightarrow \dfrac{{{Z}_{L}}}{{{Z}_{C}}}=3$
$\Rightarrow {{U}_{L}}=3{{U}_{C}}$ (1)
Ta có ${{u}_{AN}}$ sớm pha hơn ${{u}_{MB}}$ : $\dfrac{\pi }{2}$
Do đó ta có: ${{U}_{L}}+{{U}_{C}}=\sqrt{U_{AN}^{2}+U_{MB}^{2}}=40\sqrt{17}$ (V)(2)
Từ (1) và (2) $\Rightarrow {{U}_{L}}=30\sqrt{17}\text{ (V); }{{\text{U}}_{C}}=10\sqrt{17}\text{ (V)}$
Ta có: $U_{x}^{2}=U_{AN}^{2}+U_{L}^{2}-2{{U}_{AN}}{{U}_{L}}\cos \varphi $
$\Rightarrow U_{x}^{2}=U_{AN}^{2}+U_{L}^{2}-2{{U}_{AN}}{{U}_{L}}\dfrac{{{U}_{AN}}}{{{U}_{L}}+{{U}_{C}}}$
Với ${{U}_{AN}}=160\ V;{{\text{U}}_{MB}}=40\ V$.
$\Rightarrow U_{x}^{2}=50\ (V)$
Suy ra điện áp hiệu dụng giữa hai đầu đoạn mạch MN gần giá trị 48V nhất
Đáp án C.