Bài toán
Cho 3 dây dẫn song song cùng nằm trên một mp, có dòng điện chạy qua. Hỏi vị trí của một điểm M sao cho $\vec{ B_M}=\vec 0$, với M không nằm trên mp các dây, và M có khoảng cách hữu hạn tới mp chứa các dây đó.
P/s: Bài này mình vẽ hình thì thấy có tồn tại điểm M như vậy. Tuy nhiên, việc tìm điều kiện về khoảng cách làm mình gặp khó khăn.
Như đã nhận xét ở trả lời trên thì "Nếu 3 dòng điện trong dây là cùng chiều thì không có điểm M nào nằm ngoài mặt phẳng chứa dây điện thỏa yêu cầu". Như vậy, với trường hợp "có 1 dòng điện ngược chiều với hai đòng điện còn lại" thì có điểm M nào nằm ngoài mặt phẳng chứa dây điện thỏa yêu cầu không?
Ở đây, tôi khảo sát một trường hợp đơn giản là các dòng điện có cùng cường độ là $I$ và cách đều nhau.
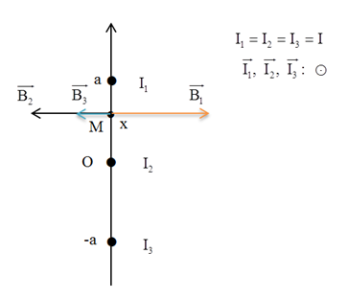
Gắn một hệ trục tọa độ như hình vẽ. Xét điểm M có tọa độ $M\left(x,y\right)$, véc tơ cảm ứng từ tại M do các dòng điện gây ra là $$\vec{B}_1=B_{1x}.\vec{i}+B_{1y}\vec{j}$$ $$\vec{B}_2=B_{2x}.\vec{i}-B_{2y}\vec{j}$$ $$\vec{B}_3=-B_{3x}.\vec{i}+B_{3y}\vec{j}$$
Suy ra, véc tơ cảm ứng từ tổng hợp tại M là $$\vec{B}=\left(B_{1x}+B_{2x}-B_{3x}\right)\vec{i}+\left(B_{1y}-B_{2x}+B_{3y}\right)\vec{j}$$
Trong đó,
$$B_{1x}=B_1.\dfrac{1-y}{\sqrt{x^2+\left(1-y\right)^2}}=\dfrac{kI\left(1-y\right)}{x^2+\left(1-y\right)^2}$$
$$B_{1y}=B_1.\dfrac{x}{\sqrt{x^2+\left(1-y\right)^2}}=\dfrac{kIx}{x^2+\left(1-y\right)^2}$$
$$B_{2x}=B_2.\dfrac{y}{\sqrt{x^2+y^2}}=\dfrac{kIy}{x^2+y^2}$$
$$B_{2y}=B_2.\dfrac{x}{\sqrt{x^2+y^2}}=\dfrac{kIx}{x^2+y^2}$$
$$B_{3x}=B_3.\dfrac{1+y}{\sqrt{x^2+\left(1+y\right)^2}}=\dfrac{kI\left(1+y\right)}{x^2+\left(1+y\right)^2}$$
$$B_{3y}=B_3.\dfrac{x}{\sqrt{x^2+\left(1+y\right)^2}}=\dfrac{kIx}{x^2+\left(1+y\right)^2}$$
Như vậy, để $\vec{B}=\vec{0}$ thì $$\left\{\begin{matrix}B_{1x}+B_{2x}=B_{3x}\\ B_{1y}+B_{3y}=B_{2y} \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
\dfrac{1-y}{x^2+\left(1-y\right)^2}+\dfrac{y}{x^2+y^2}=\dfrac{1+y}{x^2+\left(1+y\right)^2}\\ \dfrac{x}{x^2+\left(1-y\right)^2}+\dfrac{x}{x^2+\left(1+y\right)^2}=\dfrac{x}{x^2+y^2} \end{matrix}\right.$$
Bằng các phần mềm tính toán, tôi giải ra được nghiệm là $\left(1,0\right)$ và $\left(-1; 0\right)$.
Vậy, tập hợp các điểm M thỏa yêu cầu bài toán là hai đường thẳng song song nằm trong mặt phẳng vuông góc với mặt phẳng chứa các dây điện, cách dòng điện $I_2$ một khoảng bằng khoảng cách giữa hai dây điện.
Như vậy, là tồn tại và có vị trí của điểm M như vậy trong bài toán tôi khảo sát. Việc khảo sát tổng quát hơn chắc dành cho bạn nào có hứng thú chứ quan điểm của tôi là không cần thiết. :)
Linh tính về một mặt đã không đúng. :)