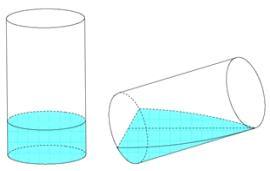
Câu hỏi: Có một cốc thủy tính hình trụ, bán kính trong lòng cốc là $4cm,$ chiều cao trong lòng cốc là $10cm$ đang đựng một lượng nước. Tính thể tích lượng nước trong cốc, biết khi nghiệm cốc nước vừa lúc chạm miệng cốc thì ở đáy mực nước trùng với đường kính đáy.
A. $\dfrac{320}{3}c{{m}^{3}}$
B. $\dfrac{320\pi }{3}c{{m}^{3}}$
C. $\dfrac{160\pi }{3}c{{m}^{3}}$
D. $\dfrac{160}{3}c{{m}^{3}}$

A. $\dfrac{320}{3}c{{m}^{3}}$
B. $\dfrac{320\pi }{3}c{{m}^{3}}$
C. $\dfrac{160\pi }{3}c{{m}^{3}}$
D. $\dfrac{160}{3}c{{m}^{3}}$
Cách giải:
Sưu tầm nhóm Toán VD - VDC

Chọn hệ trục tọa độ như hình vẽ.
Thiết diện của mặt phẳng vuông với trục $Ox$ tại $x.$ Suy ra diện tích này là tam giác $ABC$ vuông tại $B$
Ta có
$AB=BC.\tan \alpha =\sqrt{{{R}^{2}}-{{x}^{2}}}.\dfrac{h}{R}=\sqrt{4-{{x}^{2}}}.\dfrac{10}{4}$
$\Rightarrow {{S}_{\Delta ABC}}=\dfrac{1}{2}AB.BC=\dfrac{1}{2}\left( 4-{{x}^{2}} \right).\dfrac{10}{4}=\dfrac{5}{4}\left( 16-{{x}^{2}} \right)$
$\Rightarrow V=\dfrac{5}{3}\int\limits_{-4}^{4}{\left( 16-{{x}^{2}} \right)dx}=\dfrac{320}{3}\left( c{{m}^{3}} \right)$
Sưu tầm nhóm Toán VD - VDC
Chọn hệ trục tọa độ như hình vẽ.
Thiết diện của mặt phẳng vuông với trục $Ox$ tại $x.$ Suy ra diện tích này là tam giác $ABC$ vuông tại $B$
Ta có
$AB=BC.\tan \alpha =\sqrt{{{R}^{2}}-{{x}^{2}}}.\dfrac{h}{R}=\sqrt{4-{{x}^{2}}}.\dfrac{10}{4}$
$\Rightarrow {{S}_{\Delta ABC}}=\dfrac{1}{2}AB.BC=\dfrac{1}{2}\left( 4-{{x}^{2}} \right).\dfrac{10}{4}=\dfrac{5}{4}\left( 16-{{x}^{2}} \right)$
$\Rightarrow V=\dfrac{5}{3}\int\limits_{-4}^{4}{\left( 16-{{x}^{2}} \right)dx}=\dfrac{320}{3}\left( c{{m}^{3}} \right)$
Đáp án A.