Google
Câu hỏi: Cho tứ diện ABCD, lấy điểm $M$ trên cạnh AB, điểm $N$ trên cạnh AC, điểm $P$ trên cạnh CD sao cho $\dfrac{M B}{M A}=3, \dfrac{N B}{N C}=4, \dfrac{P C}{P D}=\dfrac{3}{2}$. Gọi $V_{1}, V_{2}$ theo thứ tự là thể tích các khối tứ diện MNBD và NPAC . Tính tỉ số $\dfrac{V_{1}}{V_{2}}$ ?
A. 3
B. 5
C. $\dfrac{1}{5}$
D. $\dfrac{1}{3}$
A. 3
B. 5
C. $\dfrac{1}{5}$
D. $\dfrac{1}{3}$
Phương pháp giải:
Xác định chiều cao và diện tích đáy của hai khối tứ diện MNBD và NPAC.
Áp dụng công thức tính thể tích của hình chóp có chiều cao h, diện tích đáy S thì $V=\dfrac{1}{3}h.S$.
Lập tỉ số về chiều cao và diện tích đáy của hai khối tứ diện MNBD và NPAC.
Giải chi tiết:
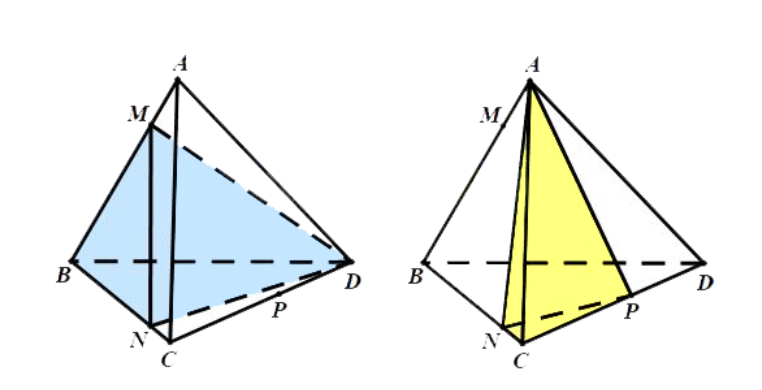Ta có:
$\begin{aligned}
& {{V}_{1}}={{V}_{MNBD}}=\dfrac{1}{3}d[M;(BCD)].{{S}_{\vartriangle NBD}}=\dfrac{1}{3}{{h}_{1}}.{{S}_{1}} \\
& {{V}_{2}}={{V}_{NBAC}}=\dfrac{1}{3}d[A;(BCD)].{{S}_{\vartriangle CNP}}=\dfrac{1}{3}{{h}_{2}}.{{S}_{2}} \\
\end{aligned}$
Suy ra, $\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{{{h}_{1}}.{{S}_{1}}}{{{h}_{2}}.{{S}_{2}}}$
Vì $\dfrac{{{h}_{1}}}{{{h}_{2}}}=\dfrac{d[M;(BCD)]}{d(A;(BCD))}=\dfrac{BM}{BA}=\dfrac{3}{4}$
${{S}_{1}}={{S}_{\vartriangle NBD}}=\dfrac{4}{5}{{S}_{\vartriangle BCD}};{{S}_{2}}={{S}_{\vartriangle CNP}}=\dfrac{1}{5}\cdot \dfrac{3}{5}{{S}_{\vartriangle BCD}}=\dfrac{3}{25}\Rightarrow \dfrac{{{S}_{1}}}{{{S}_{2}}}=\dfrac{20}{3}$
Vậy $\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{3}{4}.\dfrac{20}{3}=5$
Xác định chiều cao và diện tích đáy của hai khối tứ diện MNBD và NPAC.
Áp dụng công thức tính thể tích của hình chóp có chiều cao h, diện tích đáy S thì $V=\dfrac{1}{3}h.S$.
Lập tỉ số về chiều cao và diện tích đáy của hai khối tứ diện MNBD và NPAC.
Giải chi tiết:
$\begin{aligned}
& {{V}_{1}}={{V}_{MNBD}}=\dfrac{1}{3}d[M;(BCD)].{{S}_{\vartriangle NBD}}=\dfrac{1}{3}{{h}_{1}}.{{S}_{1}} \\
& {{V}_{2}}={{V}_{NBAC}}=\dfrac{1}{3}d[A;(BCD)].{{S}_{\vartriangle CNP}}=\dfrac{1}{3}{{h}_{2}}.{{S}_{2}} \\
\end{aligned}$
Suy ra, $\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{{{h}_{1}}.{{S}_{1}}}{{{h}_{2}}.{{S}_{2}}}$
Vì $\dfrac{{{h}_{1}}}{{{h}_{2}}}=\dfrac{d[M;(BCD)]}{d(A;(BCD))}=\dfrac{BM}{BA}=\dfrac{3}{4}$
${{S}_{1}}={{S}_{\vartriangle NBD}}=\dfrac{4}{5}{{S}_{\vartriangle BCD}};{{S}_{2}}={{S}_{\vartriangle CNP}}=\dfrac{1}{5}\cdot \dfrac{3}{5}{{S}_{\vartriangle BCD}}=\dfrac{3}{25}\Rightarrow \dfrac{{{S}_{1}}}{{{S}_{2}}}=\dfrac{20}{3}$
Vậy $\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{3}{4}.\dfrac{20}{3}=5$
Đáp án B.