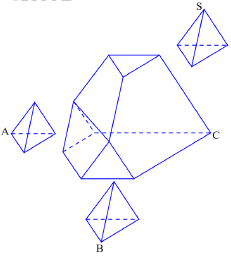
Cho một tứ diện đều $S.ABC$ có chiều cao h. Ở ba góc của tứ diện...

Phương pháp:
Chiều cao của khối tứ diện đều cạnh alà: $h=\dfrac{a\sqrt{6}}{3}$
Thể tích của khối tứ diện đều cạnh alà: $V=\dfrac{{{a}^{3}}\sqrt{2}}{12}$
Cách giải:
Tứ diện đều $S.ABC$ có chiều cao h⇒ Độ dài cạnh của tứ diện $S.ABC$ là: $\dfrac{3h}{\sqrt{6}}=\dfrac{h\sqrt{6}}{2}$
⇒ Thể tích của khối tứ diện $S.ABC$ là:
${{V}_{S.ABC}}=\dfrac{{{\left( \dfrac{h\sqrt{6}}{2} \right)}^{3}}\sqrt{2}}{12}=\dfrac{{{h}^{3}}.6\sqrt{6}.\sqrt{2}}{8.12}=\dfrac{{{h}^{3}}\sqrt{3}}{8}$
Tổng thể tích của ba khối tứ diện đều bị cắt đi là: ${{V}_{0}}=3\cdot \dfrac{{{x}^{3}}\sqrt{3}}{8}$




Vì thể tích phần còn lại bằng một nửa thể tích khối tứ diện đều ban đầu nên, ta có:
$\dfrac{3{{x}^{3}}\sqrt{3}}{8}=\dfrac{1}{2}\cdot \dfrac{{{h}^{3}}\sqrt{3}}{8}\Leftrightarrow 6{{x}^{3}}={{h}^{3}}\Leftrightarrow x=\dfrac{h}{\sqrt[3]{6}}$