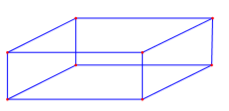
Câu hỏi: Cho một tấm nhôm hình vuông cạnh $12\left(cm \right)$. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng $x\left(cm \right)$, rồi gập tấm nhôm lại để được cái hộp không nắp (tham khảo hình vẽ bên). Tìm $x$ để hộp nhận được có thể tích lớn nhất (giải thiết bề dày tấm tôn không đáng kể).

A. $x=2$.
B. $x=3$.
C. $x=4$.
D. $x=6$.


A. $x=2$.
B. $x=3$.
C. $x=4$.
D. $x=6$.
Ta thấy hộp có đáy là hình vuông cạnh $12-2x$, đường cao $x\left(0<x<6 \right)$.
Ta có: $V={{S}_{d}}\overset{{}}{\mathop{.}} h={{\left(12-2x \right)}^{2}}\overset{{}}{\mathop{.}} x=4{{x}^{3}}-48{{x}^{2}}+144x$
Xét $V=f(x)=4{{x}^{3}}-48{{x}^{2}}+144x$
${f}'(x)=12{{x}^{2}}-96x+144=0\Rightarrow \left[ \begin{aligned}
& x=6 \\
& x=2 \\
\end{aligned} \right.\Rightarrow \left[ \begin{aligned}
& f(6)=0 \\
& f(2)=128 \\
& f(0)=0 \\
\end{aligned} \right.$
Vậy với $x=2$ hộp có thể tích lớn nhất.
Ta có: $V={{S}_{d}}\overset{{}}{\mathop{.}} h={{\left(12-2x \right)}^{2}}\overset{{}}{\mathop{.}} x=4{{x}^{3}}-48{{x}^{2}}+144x$
Xét $V=f(x)=4{{x}^{3}}-48{{x}^{2}}+144x$
${f}'(x)=12{{x}^{2}}-96x+144=0\Rightarrow \left[ \begin{aligned}
& x=6 \\
& x=2 \\
\end{aligned} \right.\Rightarrow \left[ \begin{aligned}
& f(6)=0 \\
& f(2)=128 \\
& f(0)=0 \\
\end{aligned} \right.$
Vậy với $x=2$ hộp có thể tích lớn nhất.
Đáp án A.