Câu hỏi: Cho một sợi dây đang có sóng dừng với tần số góc $\omega =20\text{ rad/s}$. Tại một điểm A trên dây là một nút sóng, điểm B là bụng sóng gần A nhất, điểm C giữa A và B. Khi sợi dây duỗi thẳng thì khoảng cách AB = 9 cm và AB = 3AC. Khi sợi dây biến dạng nhiều nhất thì khoảng cách giữa A và C là 5 cm. Tốc độ dao động của điểm B khi nó qua vị trí có li độ bằng biên độ của điểm C là
A. $160\sqrt{3}$ cm/s
B. $80\sqrt{3}$ cm/s
C. 160 cm/s
D. 80 cm/s
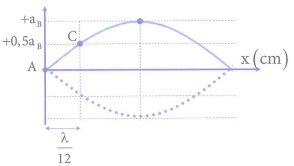
+ AB là khoảng cách giữa nút và bụng gần nhất
→ AB = 0,25λ.
Mặt khác $AB=3\text{A}C\to AC=\dfrac{\lambda }{12}$
→ điểm C dao động với biên độ bằng một nửa biên độ của bụng sóng.
+ $\lambda =4\text{A}B=36\text{ cm}$.
+ Khi sợi dây biến dạng nhiều nhất, khoảng cách giữa A và C là
$d=\sqrt{{{\left( \dfrac{\lambda }{12} \right)}^{2}}+{{\left( \dfrac{{{a}_{B}}}{2} \right)}^{2}}}=5\to {{a}_{B}}=8\text{ cm}$.
+ Khi B đi đến vị trí có li độ bằng biên độ của C ( $0,5{{\text{a}}_{B}}$ ) sẽ có tốc độ:
${{v}_{B}}=\dfrac{\sqrt{3}}{2}{{v}_{B\max }}=\dfrac{\sqrt{3}}{2}\omega {{a}_{B}}=80\sqrt{3}(\text{cm/s})$.
A. $160\sqrt{3}$ cm/s
B. $80\sqrt{3}$ cm/s
C. 160 cm/s
D. 80 cm/s
+ AB là khoảng cách giữa nút và bụng gần nhất
→ AB = 0,25λ.
Mặt khác $AB=3\text{A}C\to AC=\dfrac{\lambda }{12}$
→ điểm C dao động với biên độ bằng một nửa biên độ của bụng sóng.
+ $\lambda =4\text{A}B=36\text{ cm}$.
+ Khi sợi dây biến dạng nhiều nhất, khoảng cách giữa A và C là
$d=\sqrt{{{\left( \dfrac{\lambda }{12} \right)}^{2}}+{{\left( \dfrac{{{a}_{B}}}{2} \right)}^{2}}}=5\to {{a}_{B}}=8\text{ cm}$.
+ Khi B đi đến vị trí có li độ bằng biên độ của C ( $0,5{{\text{a}}_{B}}$ ) sẽ có tốc độ:
${{v}_{B}}=\dfrac{\sqrt{3}}{2}{{v}_{B\max }}=\dfrac{\sqrt{3}}{2}\omega {{a}_{B}}=80\sqrt{3}(\text{cm/s})$.
Đáp án B.