Câu hỏi: Cho một miếng tôn mỏng hình chữ nhật $ABCD$ với $AB=4dm$ và $AD=9dm.$ Trên cạnh $AD$ lấy điểm $E$ sao cho $AE=3dm,$ trên cạnh $BC$ lấy điểm $F$ là trung điểm của $BC$ (tham khảo hình 1). Cuộn miếng tôn lại một vòng sao cho cạnh $AB$ và $DC$ trùng khít nhau. Khi đó miếng tôn tạo thành mặt xung quanh của một hình trụ (tham khảo hình 2).
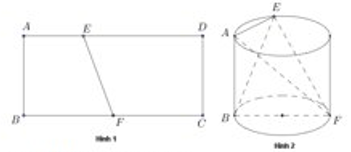
Thể tích $V$ của tứ diện $ABEF$ trong hình 2 bằng
A. $\dfrac{3\sqrt{3}}{2{{\pi }^{2}}}d{{m}^{2}}.$
B. $\dfrac{27\sqrt{3}}{2{{\pi }^{2}}}d{{m}^{2}}.$
C. $\dfrac{9\sqrt{3}}{2{{\pi }^{2}}}d{{m}^{2}}.$
D. $\dfrac{81\sqrt{3}}{2{{\pi }^{2}}}d{{m}^{2}}.$

Khi cuộn miếng tôn (hình 1) thành mặt xung quanh của hình trụ (hình 2) thì chiều cao của hình trụ bằng $h=4dm$ và chu vi đáy của hình trụ là $9dm.$
Gọi $r$ là bán kính đáy của hình trụ $\Rightarrow 2\pi r=9\Rightarrow r=\dfrac{9}{2\pi }dm.$
Độ dài đường kính $BF=2r=\dfrac{9}{\pi }dm.$
Kẻ $EM//AB\left( M\in \overrightarrow{BF} \right),$ vì $AE=\dfrac{1}{3}AD\Rightarrow \overrightarrow{AE}=\overrightarrow{BM}=\dfrac{2}{3}\overrightarrow{BF}\Rightarrow \widehat{BFM}={{60}^{0}}$ và $\widehat{MBF}={{30}^{0}}$
Tam giác $BMF$ vuông tại $M\Rightarrow BM=BF.\sin \widehat{BFM}=\dfrac{9\sqrt{3}}{2\pi }dm\Rightarrow AE=\dfrac{9\sqrt{3}}{2\pi }dm.$
Ta có $BM//AE\Rightarrow \widehat{\left( AE,BF \right)}=\widehat{MBF}={{30}^{0}}$
$\Rightarrow {{V}_{ABEF}}=\dfrac{1}{6}AE.BF.d\left( AE,BF \right).\sin \widehat{\left( AE,BF \right)}=\dfrac{1}{6}.AE.BF.AB.\sin \widehat{MBF}$
$\Rightarrow {{V}_{ABEF}}=\dfrac{27\sqrt{3}}{2{{\pi }^{2}}}d{{m}^{3}}.$

Thể tích $V$ của tứ diện $ABEF$ trong hình 2 bằng
A. $\dfrac{3\sqrt{3}}{2{{\pi }^{2}}}d{{m}^{2}}.$
B. $\dfrac{27\sqrt{3}}{2{{\pi }^{2}}}d{{m}^{2}}.$
C. $\dfrac{9\sqrt{3}}{2{{\pi }^{2}}}d{{m}^{2}}.$
D. $\dfrac{81\sqrt{3}}{2{{\pi }^{2}}}d{{m}^{2}}.$
Khi cuộn miếng tôn (hình 1) thành mặt xung quanh của hình trụ (hình 2) thì chiều cao của hình trụ bằng $h=4dm$ và chu vi đáy của hình trụ là $9dm.$
Gọi $r$ là bán kính đáy của hình trụ $\Rightarrow 2\pi r=9\Rightarrow r=\dfrac{9}{2\pi }dm.$
Độ dài đường kính $BF=2r=\dfrac{9}{\pi }dm.$
Kẻ $EM//AB\left( M\in \overrightarrow{BF} \right),$ vì $AE=\dfrac{1}{3}AD\Rightarrow \overrightarrow{AE}=\overrightarrow{BM}=\dfrac{2}{3}\overrightarrow{BF}\Rightarrow \widehat{BFM}={{60}^{0}}$ và $\widehat{MBF}={{30}^{0}}$
Tam giác $BMF$ vuông tại $M\Rightarrow BM=BF.\sin \widehat{BFM}=\dfrac{9\sqrt{3}}{2\pi }dm\Rightarrow AE=\dfrac{9\sqrt{3}}{2\pi }dm.$
Ta có $BM//AE\Rightarrow \widehat{\left( AE,BF \right)}=\widehat{MBF}={{30}^{0}}$
$\Rightarrow {{V}_{ABEF}}=\dfrac{1}{6}AE.BF.d\left( AE,BF \right).\sin \widehat{\left( AE,BF \right)}=\dfrac{1}{6}.AE.BF.AB.\sin \widehat{MBF}$
$\Rightarrow {{V}_{ABEF}}=\dfrac{27\sqrt{3}}{2{{\pi }^{2}}}d{{m}^{3}}.$
Đáp án B.