Câu hỏi: Cho mạch điện gồm: biến trở R, cuộn cảm thuần và tụ điện mắc nối tiếp (cảm kháng luôn khác dung kháng). Điện áp xoay chiều đặt vào có giá trị hiệu dụng U không đổi nhưng tần số thay đổi được. Lúc đầu, cho

A. 576W
B. 250W
C. 288W
D. 200W

A. 576W
B. 250W
C. 288W
D. 200W
Phương pháp:
+ Đọc đồ thị P-t
+ Sử dụng biểu thức tính công suất:
Cách giải:
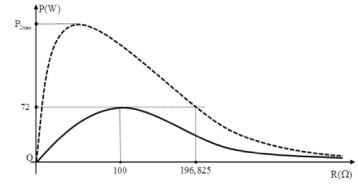
+ Khi
Với
+ Khi
Tại vị trí
Ta có:
Lại có:
+ Đọc đồ thị P-t
+ Sử dụng biểu thức tính công suất:
Cách giải:
+ Khi
Với
+ Khi
Tại vị trí
Ta có:
Lại có:
Đáp án C.