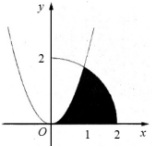
Câu hỏi: Cho $\left( H \right)$ là hình phẳng giới hạn bởi parabol $y=\sqrt{3}{{x}^{2}},$ cung tròn có phương trình $y=\sqrt{4-{{x}^{2}}}$ (với $0\le x\le 2$ ) và trục hoành (phần tô dâm trong hình vẽ bên). Khối tròn xoay tạo ra khi $\left( H \right)$ quay quanh $Ox$ có thể tích $V$ được xác định bằng công thức nào sau đây?
A. $V=\pi \int\limits_{0}^{1}{\sqrt{3}{{x}^{2}}dx}+\pi \int\limits_{1}^{2}{\sqrt{4-{{x}^{2}}}dx}$
B. $V=\pi -\int\limits_{0}^{1}{\sqrt{3}{{x}^{2}}dx}$
C. $V=\pi \int\limits_{0}^{1}{{{\left( \sqrt{4-{{x}^{2}}}-\sqrt{3}{{x}^{2}} \right)}^{2}}dx}$
D. $V=3\pi \int\limits_{0}^{1}{{{x}^{4}}dx}+\pi \int\limits_{1}^{2}{\left( 4-{{x}^{2}} \right)dx}$

A. $V=\pi \int\limits_{0}^{1}{\sqrt{3}{{x}^{2}}dx}+\pi \int\limits_{1}^{2}{\sqrt{4-{{x}^{2}}}dx}$
B. $V=\pi -\int\limits_{0}^{1}{\sqrt{3}{{x}^{2}}dx}$
C. $V=\pi \int\limits_{0}^{1}{{{\left( \sqrt{4-{{x}^{2}}}-\sqrt{3}{{x}^{2}} \right)}^{2}}dx}$
D. $V=3\pi \int\limits_{0}^{1}{{{x}^{4}}dx}+\pi \int\limits_{1}^{2}{\left( 4-{{x}^{2}} \right)dx}$
Phương pháp:
Thể tích khối tròn xoay tạo thành khi quanh hình phẳng giới hạn bởi các đường $y=f\left( x \right),y=g\left( x \right),x=a,x=b$ xung quanh trục $Ox$ là: $V=\pi \int\limits_{a}^{b}{\left| {{f}^{2}}\left( x \right)-{{g}^{2}}\left( x \right) \right|}dx.$
Cách giải:
Xét phương trình hoành độ giao điểm $\sqrt{3}{{x}^{2}}=\sqrt{4-{{x}^{2}}}\Leftrightarrow x=1.$
Thể tích cần tính: $V=\pi \int\limits_{0}^{1}{{{\left( \sqrt{3}{{x}^{2}} \right)}^{2}}dx}+\pi \int\limits_{1}^{2}{{{\left( \sqrt{4-{{x}^{2}}} \right)}^{2}}dx}=3\pi \int\limits_{0}^{1}{{{x}^{4}}dx}+\pi \int\limits_{1}^{2}{\left( 4-{{x}^{2}} \right)dx}.$
Thể tích khối tròn xoay tạo thành khi quanh hình phẳng giới hạn bởi các đường $y=f\left( x \right),y=g\left( x \right),x=a,x=b$ xung quanh trục $Ox$ là: $V=\pi \int\limits_{a}^{b}{\left| {{f}^{2}}\left( x \right)-{{g}^{2}}\left( x \right) \right|}dx.$
Cách giải:
Xét phương trình hoành độ giao điểm $\sqrt{3}{{x}^{2}}=\sqrt{4-{{x}^{2}}}\Leftrightarrow x=1.$
Thể tích cần tính: $V=\pi \int\limits_{0}^{1}{{{\left( \sqrt{3}{{x}^{2}} \right)}^{2}}dx}+\pi \int\limits_{1}^{2}{{{\left( \sqrt{4-{{x}^{2}}} \right)}^{2}}dx}=3\pi \int\limits_{0}^{1}{{{x}^{4}}dx}+\pi \int\limits_{1}^{2}{\left( 4-{{x}^{2}} \right)dx}.$
Đáp án D.