Câu hỏi: Cho lăng trụ lục giác đều có cạnh đáy bằng $2a$ và khoảng cách giữa hai đáy của lăng trụ bằng $4a.$ Tính thể tích $V$ của khối lăng trụ đã cho?
A. $V=2\sqrt{3}{{a}^{3}}$
B. $V=3\sqrt{3}{{a}^{3}}$
C. $V=6\sqrt{3}{{a}^{3}}$
D. $V=24\sqrt{3}{{a}^{3}}$
A. $V=2\sqrt{3}{{a}^{3}}$
B. $V=3\sqrt{3}{{a}^{3}}$
C. $V=6\sqrt{3}{{a}^{3}}$
D. $V=24\sqrt{3}{{a}^{3}}$
Phương pháp:
Thể tích lăng trụ bằng diện tích đáy nhân chiều cao.
Cách giải:
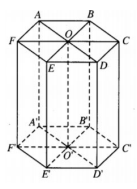
Vì $ABCDEF$ là lục giác đều nên $\Delta OAB$ là tam giác đều cạnh $2a$ (Với $O$ là tâm lục giác đều).
Ta có ${{S}_{\Delta OAB}}=\dfrac{{{\left( 2a \right)}^{2}}\sqrt{3}}{4}={{a}^{2}}\sqrt{3}$ nên ${{S}_{ABCDEF}}=6{{S}_{\Delta OAB}}=6{{a}^{2}}\sqrt{3}.$
Vậy thể tích lăng trụ là: $V=AA'.{{S}_{ABCDEF}}=4a.6{{a}^{2}}\sqrt{3}=24\sqrt{3}{{a}^{3}}.$
Thể tích lăng trụ bằng diện tích đáy nhân chiều cao.
Cách giải:
Vì $ABCDEF$ là lục giác đều nên $\Delta OAB$ là tam giác đều cạnh $2a$ (Với $O$ là tâm lục giác đều).
Ta có ${{S}_{\Delta OAB}}=\dfrac{{{\left( 2a \right)}^{2}}\sqrt{3}}{4}={{a}^{2}}\sqrt{3}$ nên ${{S}_{ABCDEF}}=6{{S}_{\Delta OAB}}=6{{a}^{2}}\sqrt{3}.$
Vậy thể tích lăng trụ là: $V=AA'.{{S}_{ABCDEF}}=4a.6{{a}^{2}}\sqrt{3}=24\sqrt{3}{{a}^{3}}.$
Đáp án D.