Câu hỏi: Cho hình chóp tứ giác $S.ABCD$ có $SA=x$ và tất cả các cạnh còn lại đều bằng 1. Khi thể tích khối chóp $S.ABCD$ đạt giá trị lớn nhất thì $x$ nhận giá trị nào sau đây?
A. $x=\dfrac{\sqrt{35}}{7}$
B. $x=1.$
C. $x=\dfrac{9}{4}$
D. $x=\dfrac{\sqrt{34}}{7}$
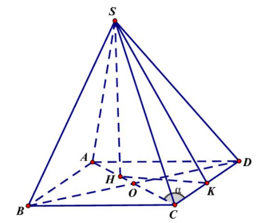
Gọi $H$ là tâm đường tròn ngoại tiếp tam giác $BCD,$ do $SB=SC=SD$ nên $SH$ là trục của đường tròn ngoại tiếp tam giác $BCD,$ suy ra $SH\bot \left( ABCD \right).$
Do tứ giác $ABCD$ là hình thoi nên $AC$ là đường trung trực của đường thẳng $BD$ do đó $H\in AC.$
Đặt $\alpha =\widehat{ACD},0<\alpha <\dfrac{\pi }{2}\Rightarrow \widehat{BCD}=2\alpha ,$ suy ra ${{S}_{ABCD}}=2{{S}_{BCD}}=BC.CD.\sin \widehat{BCD}=\sin 2\alpha .$
Gọi $K$ là trung điểm của $CD\Rightarrow CD\bot SK,$ mà $CD\bot SH$ suy ra $CD\bot HK.$
$HC=\dfrac{CK}{\cos \alpha }=\dfrac{1}{2\cos \alpha },SH=\sqrt{S{{C}^{2}}-H{{C}^{2}}}=\sqrt{1-\dfrac{1}{4{{\cos }^{2}}\alpha }}=\dfrac{\sqrt{4{{\cos }^{2}}\alpha -1}}{2\cos \alpha }$.
Thể tích khối chóp $S.ABCD$ là $V=\dfrac{1}{3}SH.{{S}_{ABCD}}=\dfrac{1}{3}\dfrac{\sqrt{4\cos \alpha -1}}{2\cos \alpha }.\sin 2\alpha =\dfrac{1}{3}\sin \alpha \sqrt{4{{\cos }^{2}}\alpha -1}$
Do đó $V=\dfrac{1}{6}\left( 2\sin \alpha \right)\sqrt{4{{\cos }^{2}}\alpha -1}\le \dfrac{1}{6}\dfrac{4{{\sin }^{2}}\alpha +4{{\cos }^{2}}\alpha -1}{2}=\dfrac{1}{4}.$
Dấu "=" xảy ra khi $2\sin \alpha =\sqrt{4{{\cos }^{2}}\alpha -1}\Leftrightarrow 4{{\sin }^{2}}\alpha =4{{\cos }^{2}}\alpha -1\Leftrightarrow {{\cos }^{2}}\alpha =\dfrac{5}{8}$
$\Leftrightarrow \cos \alpha =\dfrac{\sqrt{10}}{4}.$ Khi đó $HC=\dfrac{2}{\sqrt{10}},SH=\dfrac{\sqrt{15}}{5}.$
Gọi $O=AC\cap BD,$ suy ra $AC=2OC=2CD.\cos \alpha =\dfrac{\sqrt{10}}{2}.$
$AH=AC-HC=\dfrac{\sqrt{10}}{2}-\dfrac{2}{\sqrt{10}}=\dfrac{3}{\sqrt{10}}.$
Vậy $x=SA=\sqrt{S{{H}^{2}}+A{{H}^{2}}}=\sqrt{\dfrac{3}{5}+\dfrac{9}{10}}=\dfrac{\sqrt{6}}{2}.$
A. $x=\dfrac{\sqrt{35}}{7}$
B. $x=1.$
C. $x=\dfrac{9}{4}$
D. $x=\dfrac{\sqrt{34}}{7}$
Gọi $H$ là tâm đường tròn ngoại tiếp tam giác $BCD,$ do $SB=SC=SD$ nên $SH$ là trục của đường tròn ngoại tiếp tam giác $BCD,$ suy ra $SH\bot \left( ABCD \right).$
Do tứ giác $ABCD$ là hình thoi nên $AC$ là đường trung trực của đường thẳng $BD$ do đó $H\in AC.$
Đặt $\alpha =\widehat{ACD},0<\alpha <\dfrac{\pi }{2}\Rightarrow \widehat{BCD}=2\alpha ,$ suy ra ${{S}_{ABCD}}=2{{S}_{BCD}}=BC.CD.\sin \widehat{BCD}=\sin 2\alpha .$
Gọi $K$ là trung điểm của $CD\Rightarrow CD\bot SK,$ mà $CD\bot SH$ suy ra $CD\bot HK.$
$HC=\dfrac{CK}{\cos \alpha }=\dfrac{1}{2\cos \alpha },SH=\sqrt{S{{C}^{2}}-H{{C}^{2}}}=\sqrt{1-\dfrac{1}{4{{\cos }^{2}}\alpha }}=\dfrac{\sqrt{4{{\cos }^{2}}\alpha -1}}{2\cos \alpha }$.
Thể tích khối chóp $S.ABCD$ là $V=\dfrac{1}{3}SH.{{S}_{ABCD}}=\dfrac{1}{3}\dfrac{\sqrt{4\cos \alpha -1}}{2\cos \alpha }.\sin 2\alpha =\dfrac{1}{3}\sin \alpha \sqrt{4{{\cos }^{2}}\alpha -1}$
Do đó $V=\dfrac{1}{6}\left( 2\sin \alpha \right)\sqrt{4{{\cos }^{2}}\alpha -1}\le \dfrac{1}{6}\dfrac{4{{\sin }^{2}}\alpha +4{{\cos }^{2}}\alpha -1}{2}=\dfrac{1}{4}.$
Dấu "=" xảy ra khi $2\sin \alpha =\sqrt{4{{\cos }^{2}}\alpha -1}\Leftrightarrow 4{{\sin }^{2}}\alpha =4{{\cos }^{2}}\alpha -1\Leftrightarrow {{\cos }^{2}}\alpha =\dfrac{5}{8}$
$\Leftrightarrow \cos \alpha =\dfrac{\sqrt{10}}{4}.$ Khi đó $HC=\dfrac{2}{\sqrt{10}},SH=\dfrac{\sqrt{15}}{5}.$
Gọi $O=AC\cap BD,$ suy ra $AC=2OC=2CD.\cos \alpha =\dfrac{\sqrt{10}}{2}.$
$AH=AC-HC=\dfrac{\sqrt{10}}{2}-\dfrac{2}{\sqrt{10}}=\dfrac{3}{\sqrt{10}}.$
Vậy $x=SA=\sqrt{S{{H}^{2}}+A{{H}^{2}}}=\sqrt{\dfrac{3}{5}+\dfrac{9}{10}}=\dfrac{\sqrt{6}}{2}.$
Đáp án D.