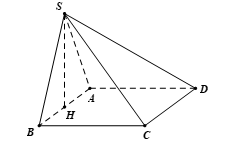
Câu hỏi: Cho hình chóp tứ giác $S.ABCD$ có đáy là hình vuông cạnh $a\sqrt{2}$, tam giác $SAB$ đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp đã cho.
A. $\dfrac{{{a}^{3}}\sqrt{6}}{3}$.
B. $\dfrac{2{{a}^{3}}\sqrt{6}}{3}$.
C. $\dfrac{{{a}^{3}}\sqrt{3}}{2}$.
D. $\dfrac{{{a}^{3}}\sqrt{6}}{6}$.

A. $\dfrac{{{a}^{3}}\sqrt{6}}{3}$.
B. $\dfrac{2{{a}^{3}}\sqrt{6}}{3}$.
C. $\dfrac{{{a}^{3}}\sqrt{3}}{2}$.
D. $\dfrac{{{a}^{3}}\sqrt{6}}{6}$.
Gọi $H$ là trung điểm của $AB\Rightarrow SH\bot \left( ABCD \right)$.
$\Rightarrow {{V}_{S.ABCD}}=\dfrac{1}{3}{{S}_{ABCD}}\cdot SH=\dfrac{1}{3}\cdot {{\left( a\sqrt{2} \right)}^{2}}\cdot \dfrac{a\sqrt{6}}{2}$ $=\dfrac{{{a}^{3}}\sqrt{6}}{3}$.
$\Rightarrow {{V}_{S.ABCD}}=\dfrac{1}{3}{{S}_{ABCD}}\cdot SH=\dfrac{1}{3}\cdot {{\left( a\sqrt{2} \right)}^{2}}\cdot \dfrac{a\sqrt{6}}{2}$ $=\dfrac{{{a}^{3}}\sqrt{6}}{3}$.
Đáp án A.