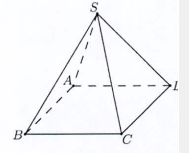
Câu hỏi: Cho hình chóp tứ giác đều $S.ABCD$ có độ dài cạnh đáy bằng $2$ và độ dài cạnh bên bằng 3 (tham khảo hình bên). Khoảng cách từ $S$ đến mặt phẳng $\left( ABCD \right)$ bằng
A. $\sqrt{7}.$
B. 1.
C. 7.
D. $\sqrt{11}.$

A. $\sqrt{7}.$
B. 1.
C. 7.
D. $\sqrt{11}.$
Cách giải:

Gọi $\left\{ O \right\}=AC\cap BD.$ Vì $S.ABCD$ là chóp tứ giác đều nên $SO\bot \left( ABCD \right),$ do đó $d\left( S;\left( ABCD \right) \right)=SO.$
Vì $ABCD$ là hình vuông cạnh 2 nên $BD=2\sqrt{2}\Rightarrow OD=\sqrt{2}.$
Áp dụng định lý Pytago trong tam giác vuông $SOD$ ta có:
$SO=\sqrt{S{{D}^{2}}-O{{D}^{2}}}=\sqrt{9-2}=\sqrt{7}$
Vậy $d\left( S;\left( ABCD \right) \right)=\sqrt{7}.$
Gọi $\left\{ O \right\}=AC\cap BD.$ Vì $S.ABCD$ là chóp tứ giác đều nên $SO\bot \left( ABCD \right),$ do đó $d\left( S;\left( ABCD \right) \right)=SO.$
Vì $ABCD$ là hình vuông cạnh 2 nên $BD=2\sqrt{2}\Rightarrow OD=\sqrt{2}.$
Áp dụng định lý Pytago trong tam giác vuông $SOD$ ta có:
$SO=\sqrt{S{{D}^{2}}-O{{D}^{2}}}=\sqrt{9-2}=\sqrt{7}$
Vậy $d\left( S;\left( ABCD \right) \right)=\sqrt{7}.$
Đáp án A.