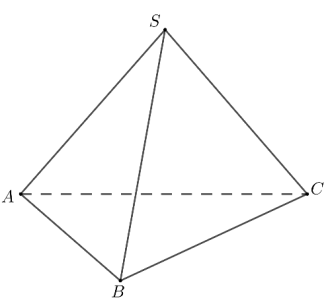
Câu hỏi: Cho hình chóp tam giác đều $S.ABC$ cạnh đáy bằng $a$ và khoảng cách từ $A$ đến mặt phẳng $(SBC)$ bằng $\dfrac{3a}{4}$ (tham khảo hình vẽ bên dưới). Góc giữa mặt phẳng $(SBC)$ với mặt phẳng đáy $(ABC)$ bằng
A. ${{30}^{0}}$.
B. ${{45}^{0}}$.
C. ${{60}^{0}}$.
D. ${{90}^{0}}$.

Gọi $D$ là trung điểm của $BC,AD\bot BC$ và $AD=\dfrac{a\sqrt{3}}{2}$ (do $\Delta ABC$ đều cạnh $a$ ).
Hình chóp tam giác đều $S.ABC\Rightarrow \Delta SBC$ cân tại $S\Rightarrow SD\bot BC.$
Do $AD\bot BC$ và $SD\bot BC\Rightarrow BC\bot \left( SAD \right)$.
Kẻ $AH\bot SD$ tại $H\Rightarrow AH\bot BC$ (do $BC\bot \left( SAD \right)$ ).
Vì $AH\bot SD$ và $AH\bot BC\Rightarrow AH\bot \left( SBC \right)\Rightarrow AH={{d}_{\left( A;\left( SBC \right) \right)}}=\dfrac{3a}{4}.$
Như vậy: $\widehat{\left( \left( SBC \right);\left( ABC \right) \right)}=\widehat{SDA}$.
$\Delta AHD$ vuông tại $H\Rightarrow \sin \widehat{SDA}=\dfrac{AH}{AD}=\dfrac{3a}{4};\dfrac{a\sqrt{3}}{2}=\dfrac{\sqrt{3}}{2}\Rightarrow \widehat{SDA}={{60}^{0}}$.
Vậy góc giữa mặt phẳng $\left( SBC \right)$ với mặt phẳng đáy $\left( ABC \right)$ bằng ${{60}^{0}}$.

A. ${{30}^{0}}$.
B. ${{45}^{0}}$.
C. ${{60}^{0}}$.
D. ${{90}^{0}}$.
Gọi $D$ là trung điểm của $BC,AD\bot BC$ và $AD=\dfrac{a\sqrt{3}}{2}$ (do $\Delta ABC$ đều cạnh $a$ ).
Hình chóp tam giác đều $S.ABC\Rightarrow \Delta SBC$ cân tại $S\Rightarrow SD\bot BC.$
Do $AD\bot BC$ và $SD\bot BC\Rightarrow BC\bot \left( SAD \right)$.
Kẻ $AH\bot SD$ tại $H\Rightarrow AH\bot BC$ (do $BC\bot \left( SAD \right)$ ).
Vì $AH\bot SD$ và $AH\bot BC\Rightarrow AH\bot \left( SBC \right)\Rightarrow AH={{d}_{\left( A;\left( SBC \right) \right)}}=\dfrac{3a}{4}.$
Như vậy: $\widehat{\left( \left( SBC \right);\left( ABC \right) \right)}=\widehat{SDA}$.
$\Delta AHD$ vuông tại $H\Rightarrow \sin \widehat{SDA}=\dfrac{AH}{AD}=\dfrac{3a}{4};\dfrac{a\sqrt{3}}{2}=\dfrac{\sqrt{3}}{2}\Rightarrow \widehat{SDA}={{60}^{0}}$.
Vậy góc giữa mặt phẳng $\left( SBC \right)$ với mặt phẳng đáy $\left( ABC \right)$ bằng ${{60}^{0}}$.
Đáp án C.