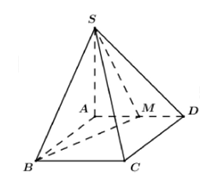
Câu hỏi: Cho hình chóp $S.ABCD$ có đáy là hình chữ nhật $AB=a,AD=2a,SA$ vuông góc với mặt phẳng đáy và $SA=a.$ Gọi $M$ là trung điểm của $AD.$ Tính khoảng cách giữa hai đường thẳng $BM$ và $SD.$
A. $\dfrac{a\sqrt{2}}{2}$
B. $\dfrac{a\sqrt{6}}{3}$
C. $\dfrac{a\sqrt{6}}{6}$
D. $\dfrac{2a\sqrt{5}}{5}$

A. $\dfrac{a\sqrt{2}}{2}$
B. $\dfrac{a\sqrt{6}}{3}$
C. $\dfrac{a\sqrt{6}}{6}$
D. $\dfrac{2a\sqrt{5}}{5}$
Phương pháp:
- Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách từ đường thẳng này đến mặt phẳng song song và chứa đường thẳng kia, gọi $N$ là trung điểm của $Bc,$ chứng minh $d\left( BM;SD \right)=d\left( M;\left( SDN \right) \right).$
- Đổi tính khoảng cách từ $M$ đến $\left( SDN \right)$ sang tính khoảng cách từ $A$ đến $\left( SDN \right).$
- Chứng minh $DN\bot \left( SAN \right).$
- Trong $\left( SAN \right)$ kẻ $AN\bot SN,$ chứng minh $AH\bot \left( SDN \right).$
- Sử dụng hệ thức lượng trong tam giác vuông và tính chất tam giác vuông cân để tính khoảng cách.
Cách giải:

Gọi $N$ là trung điểm của $BC$ ta có: $\left\{ \begin{aligned}
& DM=BN \\
& DM//BN \\
\end{aligned} \right.\Rightarrow BNDM $ là hình bình hành $ \Rightarrow BM//DN.$
$\Rightarrow BM//\left( SDN \right)\supset SD\Rightarrow d\left( BM;SD \right)=d\left( BM;\left( SDN \right) \right)=d\left( M;\left( SDN \right) \right).$
Ta có: $AM\cap \left( SDN \right)=D\Rightarrow \dfrac{d\left( M;\left( SDN \right) \right)}{d\left( A;\left( SDN \right) \right)}=\dfrac{MD}{AD}=\dfrac{1}{2}\Rightarrow d\left( M;\left( SDN \right) \right)=\dfrac{1}{2}d\left( A;\left( SDN \right) \right).$
Trong $\left( ABCD \right)$ gọi $I$ là trung điểm của $BM.$
Ta có $\left\{ \begin{aligned}
& AM=BN \\
& AM//BN \\
\end{aligned} \right.\Rightarrow AMNB $ là hình bình hành, do đó hai đường chéo cắt nhau tại trung điểm mỗi đường nên $ I $ cũng là trung điểm của $ AN, $ hay $ A,I,N$ thẳng hàng.
Xét $\Delta ABM$ có $AB=AM=a\Rightarrow \Delta ABM$ vuông cân tại $A\Rightarrow AI\bot BM\Rightarrow AN\bot DN.$
Ta có: $\left\{ \begin{aligned}
& DN\bot AN \\
& DN\bot SA \\
\end{aligned} \right.\Rightarrow DN\bot \left( SAN \right).$
Trong $\left( SAN \right)$ kẻ $AH\bot SN\left( H\in SN \right)$ ta có $\left\{ \begin{aligned}
& AH\bot SN \\
& AH\bot DN \\
\end{aligned} \right.\Rightarrow AH\bot \left( SDN \right)\Rightarrow d\left( A;\left( SDN \right) \right)=AH.$
Tam giác $ABM$ vuông cân cạnh $a\Rightarrow BM=a\sqrt{2}=AN.$
Áp dụng hệ thức lượng trong tam giác vuông $SAN$ có: $AH=\dfrac{SA.AN}{\sqrt{S{{A}^{2}}+A{{N}^{2}}}}=\dfrac{a.a\sqrt{2}}{\sqrt{{{a}^{2}}+2{{a}^{2}}}}=\dfrac{a\sqrt{6}}{3}.$
Vậy $d\left( BM;SD \right)=\dfrac{1}{2}AH=\dfrac{a\sqrt{6}}{6}.$
- Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách từ đường thẳng này đến mặt phẳng song song và chứa đường thẳng kia, gọi $N$ là trung điểm của $Bc,$ chứng minh $d\left( BM;SD \right)=d\left( M;\left( SDN \right) \right).$
- Đổi tính khoảng cách từ $M$ đến $\left( SDN \right)$ sang tính khoảng cách từ $A$ đến $\left( SDN \right).$
- Chứng minh $DN\bot \left( SAN \right).$
- Trong $\left( SAN \right)$ kẻ $AN\bot SN,$ chứng minh $AH\bot \left( SDN \right).$
- Sử dụng hệ thức lượng trong tam giác vuông và tính chất tam giác vuông cân để tính khoảng cách.
Cách giải:
Gọi $N$ là trung điểm của $BC$ ta có: $\left\{ \begin{aligned}
& DM=BN \\
& DM//BN \\
\end{aligned} \right.\Rightarrow BNDM $ là hình bình hành $ \Rightarrow BM//DN.$
$\Rightarrow BM//\left( SDN \right)\supset SD\Rightarrow d\left( BM;SD \right)=d\left( BM;\left( SDN \right) \right)=d\left( M;\left( SDN \right) \right).$
Ta có: $AM\cap \left( SDN \right)=D\Rightarrow \dfrac{d\left( M;\left( SDN \right) \right)}{d\left( A;\left( SDN \right) \right)}=\dfrac{MD}{AD}=\dfrac{1}{2}\Rightarrow d\left( M;\left( SDN \right) \right)=\dfrac{1}{2}d\left( A;\left( SDN \right) \right).$
Trong $\left( ABCD \right)$ gọi $I$ là trung điểm của $BM.$
Ta có $\left\{ \begin{aligned}
& AM=BN \\
& AM//BN \\
\end{aligned} \right.\Rightarrow AMNB $ là hình bình hành, do đó hai đường chéo cắt nhau tại trung điểm mỗi đường nên $ I $ cũng là trung điểm của $ AN, $ hay $ A,I,N$ thẳng hàng.
Xét $\Delta ABM$ có $AB=AM=a\Rightarrow \Delta ABM$ vuông cân tại $A\Rightarrow AI\bot BM\Rightarrow AN\bot DN.$
Ta có: $\left\{ \begin{aligned}
& DN\bot AN \\
& DN\bot SA \\
\end{aligned} \right.\Rightarrow DN\bot \left( SAN \right).$
Trong $\left( SAN \right)$ kẻ $AH\bot SN\left( H\in SN \right)$ ta có $\left\{ \begin{aligned}
& AH\bot SN \\
& AH\bot DN \\
\end{aligned} \right.\Rightarrow AH\bot \left( SDN \right)\Rightarrow d\left( A;\left( SDN \right) \right)=AH.$
Tam giác $ABM$ vuông cân cạnh $a\Rightarrow BM=a\sqrt{2}=AN.$
Áp dụng hệ thức lượng trong tam giác vuông $SAN$ có: $AH=\dfrac{SA.AN}{\sqrt{S{{A}^{2}}+A{{N}^{2}}}}=\dfrac{a.a\sqrt{2}}{\sqrt{{{a}^{2}}+2{{a}^{2}}}}=\dfrac{a\sqrt{6}}{3}.$
Vậy $d\left( BM;SD \right)=\dfrac{1}{2}AH=\dfrac{a\sqrt{6}}{6}.$
Đáp án C.