Câu hỏi: Cho hình chóp $S. ABCD$ có đáy $ABCD$ là hình thang vuông tại $B$ và $C$, $CD=2AB, AD=a, \widehat{ADC}=30{}^\circ $, $SA$ vuông góc với mặt phẳng đáy và $SA=2a$ (minh họa như hình bên dưới).
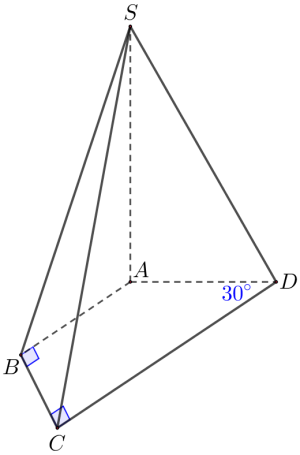
Khoảng cách từ $D$ đến mặt phẳng $\left(SBC \right)$ bằng
A. $\dfrac{2\sqrt{57}a}{19}$.
B. $\dfrac{\sqrt{57}a}{19}$.
C. $\dfrac{4\sqrt{57}a}{19}$.
D. $\sqrt{3}a$.

Khoảng cách từ $D$ đến mặt phẳng $\left(SBC \right)$ bằng
A. $\dfrac{2\sqrt{57}a}{19}$.
B. $\dfrac{\sqrt{57}a}{19}$.
C. $\dfrac{4\sqrt{57}a}{19}$.
D. $\sqrt{3}a$.
Gọi $E$ là trung điểm $CD$. Ta có tứ giác $ABCE$ là hình chữ nhật.
Ta có: $d\left(D,\left( SBC \right) \right)=2d\left(E,\left( SBC \right) \right)$.
Do: $AE \text{//} BC\Rightarrow d\left(E,\left( SBC \right) \right)=d\left(A,\left( SBC \right) \right)$.
Kẻ $AH\bot SB$ tại $H$. Ta có: $\left\{ \begin{aligned}
& BC\bot AB \\
& BC\bot SA \\
\end{aligned} \right.\Rightarrow BC\bot \left(SAB \right)\Rightarrow BC\bot AH$.
Do đó: $\left\{ \begin{aligned}
& AH\bot SB \\
& AH\bot BC \\
\end{aligned} \right.\Rightarrow AH\bot \left(SBC \right)\Rightarrow d\left(A,\left( SBC \right) \right)=AH$.
Ta có: $\dfrac{1}{A{{H}^{2}}}=\dfrac{1}{A{{B}^{2}}}+\dfrac{1}{A{{S}^{2}}}$ với: $AB=CE=ED=AD.\cos \widehat{ADE}=\dfrac{a\sqrt{3}}{2}$ ; $AS=2a$.
$\Rightarrow \dfrac{1}{A{{H}^{2}}}=\dfrac{4}{3{{a}^{2}}}+\dfrac{1}{4{{a}^{2}}}=\dfrac{19}{12{{a}^{2}}}\Rightarrow AH=\dfrac{2a\sqrt{57}}{19}$.
Vậy: $d\left(D,\left( SBC \right) \right)=\dfrac{4\sqrt{57}a}{19}$.
Ta có: $d\left(D,\left( SBC \right) \right)=2d\left(E,\left( SBC \right) \right)$.
Do: $AE \text{//} BC\Rightarrow d\left(E,\left( SBC \right) \right)=d\left(A,\left( SBC \right) \right)$.
Kẻ $AH\bot SB$ tại $H$. Ta có: $\left\{ \begin{aligned}
& BC\bot AB \\
& BC\bot SA \\
\end{aligned} \right.\Rightarrow BC\bot \left(SAB \right)\Rightarrow BC\bot AH$.
Do đó: $\left\{ \begin{aligned}
& AH\bot SB \\
& AH\bot BC \\
\end{aligned} \right.\Rightarrow AH\bot \left(SBC \right)\Rightarrow d\left(A,\left( SBC \right) \right)=AH$.
Ta có: $\dfrac{1}{A{{H}^{2}}}=\dfrac{1}{A{{B}^{2}}}+\dfrac{1}{A{{S}^{2}}}$ với: $AB=CE=ED=AD.\cos \widehat{ADE}=\dfrac{a\sqrt{3}}{2}$ ; $AS=2a$.
$\Rightarrow \dfrac{1}{A{{H}^{2}}}=\dfrac{4}{3{{a}^{2}}}+\dfrac{1}{4{{a}^{2}}}=\dfrac{19}{12{{a}^{2}}}\Rightarrow AH=\dfrac{2a\sqrt{57}}{19}$.
Vậy: $d\left(D,\left( SBC \right) \right)=\dfrac{4\sqrt{57}a}{19}$.
Đáp án C.