Câu hỏi: Cho hình chóp $S. ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$ và $D$, $AB=AD=2a; DC=a$. Điểm $I$ là trung điểm đoạn $AD$, mặt phẳng $\left(SIB \right)$ và $\left(SIC \right)$ cùng vuông góc với mặt phẳng $\left(ABCD \right)$. Mặt phẳng $\left(SBC \right)$ tạo với mặt phẳng $\left(ABCD \right)$ một góc $60{}^\circ $. Tính khoảng cách từ $D$ đến $\left(SBC \right)$ theo $a$.
A. $\frac{a\sqrt{15}}{5}$.
B. $\frac{9a\sqrt{15}}{10}$.
C. $\frac{2a\sqrt{15}}{5}$.
D. $\frac{9a\sqrt{15}}{20}$.

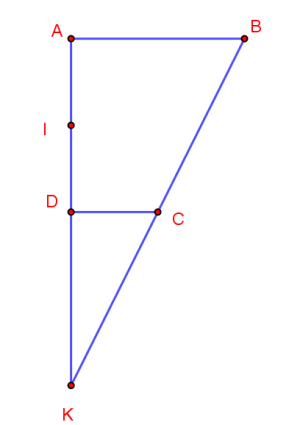
Vì mặt phẳng $\left( SIB \right)$ và $\left( SIC \right)$ cùng vuông góc với mặt phẳng $\left( ABCD \right)$ và $\left( SIB \right)\cap \left( SIC \right)=SI$ nên $SI\bot \left( ABCD \right)$.
Trong mặt phẳng $\left( ABCD \right)$, gọi $E$ là hình chiếu vuông góc của $I$ trên $BC$. Khi đó, $\left( \widehat{\left( SBC \right),\left( ABCD \right)} \right)=\left( \widehat{SE,IE} \right)=\widehat{SEI}=60{}^\circ $.
Ta có $IB=\sqrt{I{{A}^{2}}+A{{B}^{2}}}=a\sqrt{5}$, $IC=\sqrt{I{{D}^{2}}+D{{C}^{2}}}=a\sqrt{2}$ và $BC=a\sqrt{5}$.
Áp dụng công thức Hê-rông, diện tích tam giác $IBC$ là ${{S}_{IBC}}=\frac{3{{a}^{2}}}{2}$.
Mà ${{S}_{IBC}}=\frac{1}{2}IE.BC\Rightarrow IE=\frac{3a\sqrt{5}}{5}$.
Trong mặt phẳng $\left( SIE \right)$, gọi $H$ là chân đường cao kẻ từ $I$ của tam giác $SIE$.
Vì $\left\{ \begin{aligned}
& \left( SIE \right)\bot \left( SBC \right) \\
& \left( SIE \right)\cap \left( SBC \right)=SE \\
& \left( SIE \right)\supset IH\bot SE \\
\end{aligned} \right.\Rightarrow IH\bot \left( SBC \right) $, suy ra $ d\left( I,\left( SBC \right) \right)=IH $.
Tam giác $IHE$ vuông tại $H$ có $IH=IE.\sin 60{}^\circ =\frac{3a\sqrt{15}}{10}$.
Mặt khác $\frac{d\left( D,\left( SBC \right) \right)}{d\left( I,\left( SBC \right) \right)}=\frac{KD}{KI}=\frac{2}{3}\Rightarrow d\left( D,\left( SBC \right) \right)=\frac{2}{3}d\left( I,\left( SBC \right) \right)=\frac{2}{3}.\frac{3a\sqrt{15}}{10}=\frac{a\sqrt{15}}{5}$.
A. $\frac{a\sqrt{15}}{5}$.
B. $\frac{9a\sqrt{15}}{10}$.
C. $\frac{2a\sqrt{15}}{5}$.
D. $\frac{9a\sqrt{15}}{20}$.

Vì mặt phẳng $\left( SIB \right)$ và $\left( SIC \right)$ cùng vuông góc với mặt phẳng $\left( ABCD \right)$ và $\left( SIB \right)\cap \left( SIC \right)=SI$ nên $SI\bot \left( ABCD \right)$.
Trong mặt phẳng $\left( ABCD \right)$, gọi $E$ là hình chiếu vuông góc của $I$ trên $BC$. Khi đó, $\left( \widehat{\left( SBC \right),\left( ABCD \right)} \right)=\left( \widehat{SE,IE} \right)=\widehat{SEI}=60{}^\circ $.
Ta có $IB=\sqrt{I{{A}^{2}}+A{{B}^{2}}}=a\sqrt{5}$, $IC=\sqrt{I{{D}^{2}}+D{{C}^{2}}}=a\sqrt{2}$ và $BC=a\sqrt{5}$.
Áp dụng công thức Hê-rông, diện tích tam giác $IBC$ là ${{S}_{IBC}}=\frac{3{{a}^{2}}}{2}$.
Mà ${{S}_{IBC}}=\frac{1}{2}IE.BC\Rightarrow IE=\frac{3a\sqrt{5}}{5}$.
Trong mặt phẳng $\left( SIE \right)$, gọi $H$ là chân đường cao kẻ từ $I$ của tam giác $SIE$.
Vì $\left\{ \begin{aligned}
& \left( SIE \right)\bot \left( SBC \right) \\
& \left( SIE \right)\cap \left( SBC \right)=SE \\
& \left( SIE \right)\supset IH\bot SE \\
\end{aligned} \right.\Rightarrow IH\bot \left( SBC \right) $, suy ra $ d\left( I,\left( SBC \right) \right)=IH $.
Tam giác $IHE$ vuông tại $H$ có $IH=IE.\sin 60{}^\circ =\frac{3a\sqrt{15}}{10}$.
Mặt khác $\frac{d\left( D,\left( SBC \right) \right)}{d\left( I,\left( SBC \right) \right)}=\frac{KD}{KI}=\frac{2}{3}\Rightarrow d\left( D,\left( SBC \right) \right)=\frac{2}{3}d\left( I,\left( SBC \right) \right)=\frac{2}{3}.\frac{3a\sqrt{15}}{10}=\frac{a\sqrt{15}}{5}$.
Đáp án A.