Google
Câu hỏi: Cho hình chóp $S.ABC$ đáy $ABC$ là tam giác vuông tại $B,AB=a;BC=a\sqrt{3}$ có hai mặt phẳng $\left( SAB \right);\left( SAC \right)$ cùng vuông góc với đáy. Góc giữa $SC$ với mặt đáy bằng ${{60}^{\circ }}$. Tính khoảng cách từ $A$ đến mặt $\left( SBC \right)$.
A. $\dfrac{2a\sqrt{39}}{13}$.
B. $\dfrac{a\sqrt{39}}{13}$.
C. $\dfrac{2a\sqrt{39}}{39}$.
D. $\dfrac{4a\sqrt{39}}{13}$.
A. $\dfrac{2a\sqrt{39}}{13}$.
B. $\dfrac{a\sqrt{39}}{13}$.
C. $\dfrac{2a\sqrt{39}}{39}$.
D. $\dfrac{4a\sqrt{39}}{13}$.
Phương pháp:
$\left\{ \begin{aligned}
& \left( P \right)\cap \left( Q \right)=d \\
& \left( P \right)\bot \left( \alpha \right) \\
& \left( Q \right)\bot \left( \alpha \right) \\
\end{aligned} \right.\Rightarrow d\bot \left( \alpha \right)$
Cách giải:
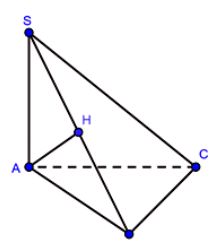$\left( SAB \right),\left( SAC \right)$ cùng vuông góc với đáy $\Rightarrow SA\bot \left( ABC \right)$.
$\Rightarrow \left( SC;\left( ABC \right) \right)=SCA={{60}^{0}}.$
Ta có: $\left\{ \begin{aligned}
& BC\bot AB \\
& BC\bot SA \\
\end{aligned} \right.\Rightarrow BC\bot \left( SAB \right)$
Kẻ $AH\bot SB$, mà $AH\bot BC\Rightarrow AH\bot \left( SBC \right)\Rightarrow d\left( A;\left( SBC \right) \right)=AH$.
Tam giác $ABC$ vuông tại $B\Rightarrow AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=\sqrt{{{a}^{2}}+3{{a}^{2}}}=2a.$
Tam giác $SAC$ vuông tại $A\Rightarrow AB=AC\tan C=2a.\tan {{60}^{0}}=2a\sqrt{3}$.
Tam giác $SAB$ vuông tại $A$, đường cao $AH\Rightarrow \dfrac{1}{A{{H}^{2}}}=\dfrac{1}{S{{A}^{2}}}+\dfrac{1}{A{{B}^{2}}}=\dfrac{1}{12{{a}^{2}}}+\dfrac{1}{{{a}^{2}}}=\dfrac{13}{12{{a}^{2}}}\Rightarrow AH=\sqrt{\dfrac{12}{13}}a=\dfrac{2a\sqrt{39}}{13}$
Vậy khoảng cách từ $A$ đến mặt phẳng $\left( SBC \right)$ là: $\dfrac{2a\sqrt{39}}{13}$.
$\left\{ \begin{aligned}
& \left( P \right)\cap \left( Q \right)=d \\
& \left( P \right)\bot \left( \alpha \right) \\
& \left( Q \right)\bot \left( \alpha \right) \\
\end{aligned} \right.\Rightarrow d\bot \left( \alpha \right)$
Cách giải:
$\Rightarrow \left( SC;\left( ABC \right) \right)=SCA={{60}^{0}}.$
Ta có: $\left\{ \begin{aligned}
& BC\bot AB \\
& BC\bot SA \\
\end{aligned} \right.\Rightarrow BC\bot \left( SAB \right)$
Kẻ $AH\bot SB$, mà $AH\bot BC\Rightarrow AH\bot \left( SBC \right)\Rightarrow d\left( A;\left( SBC \right) \right)=AH$.
Tam giác $ABC$ vuông tại $B\Rightarrow AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=\sqrt{{{a}^{2}}+3{{a}^{2}}}=2a.$
Tam giác $SAC$ vuông tại $A\Rightarrow AB=AC\tan C=2a.\tan {{60}^{0}}=2a\sqrt{3}$.
Tam giác $SAB$ vuông tại $A$, đường cao $AH\Rightarrow \dfrac{1}{A{{H}^{2}}}=\dfrac{1}{S{{A}^{2}}}+\dfrac{1}{A{{B}^{2}}}=\dfrac{1}{12{{a}^{2}}}+\dfrac{1}{{{a}^{2}}}=\dfrac{13}{12{{a}^{2}}}\Rightarrow AH=\sqrt{\dfrac{12}{13}}a=\dfrac{2a\sqrt{39}}{13}$
Vậy khoảng cách từ $A$ đến mặt phẳng $\left( SBC \right)$ là: $\dfrac{2a\sqrt{39}}{13}$.
Đáp án A.