Google
Câu hỏi: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều, $\left( SAB \right)$ vuông góc với đáy $\left( ABC \right)$ và tam giác $SAB$ đều, khoảng cách từ điểm $A$ tới mặt phẳng $\left( SCB \right)$ bằng $\dfrac{2\sqrt{15}}{5}a$. Thể tích của khối chóp $S.ABC$ là
A. $\dfrac{{{a}^{3}}}{8}$.
B. $\dfrac{3{{a}^{3}}}{8}$.
C. $\dfrac{{{a}^{3}}}{3}$.
D. ${{a}^{3}}$.
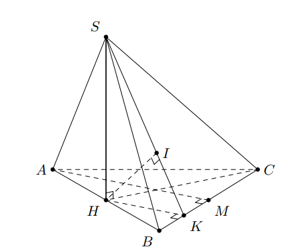Gọi $H$ và $M$ lần lượt là trung điểm của $AB$ và $BC$.
Gọi $K$ là trung điểm của $BM\Rightarrow HK\bot BM$.
Gọi $I$ là hình chiếu của $H$ lên $SK$ suy ra $HI\bot \left( SBC \right)$.
Khi đó $HI=\text{d}\left( H,\left( SBC \right) \right)=\dfrac{1}{2}\text{d}\left( A,\left( SBC \right) \right)=\dfrac{\sqrt{15}}{5}a$.
Đặt $AB=x$ suy ra $SH=AM=\dfrac{x\sqrt{3}}{2}$ và $HK=\dfrac{1}{2}AM=\dfrac{x\sqrt{3}}{4}$.
Do đó
$\dfrac{1}{H{{I}^{2}}}=\dfrac{1}{H{{S}^{2}}}+\dfrac{1}{H{{K}^{2}}}\Leftrightarrow \dfrac{1}{{{\left( \dfrac{a\sqrt{15}}{5} \right)}^{2}}}=\dfrac{1}{{{\left( \dfrac{x\sqrt{3}}{2} \right)}^{2}}}+\dfrac{1}{{{\left( \dfrac{x\sqrt{3}}{4} \right)}^{2}}}\Leftrightarrow x=2a$.
Vậy $V=\dfrac{1}{3}\cdot {{S}_{ABC}}\cdot SH=\dfrac{1}{3}\cdot \dfrac{{{x}^{2}}\sqrt{3}}{4}\cdot \dfrac{x\sqrt{3}}{2}=\dfrac{{{x}^{3}}}{8}={{a}^{3}}$.
A. $\dfrac{{{a}^{3}}}{8}$.
B. $\dfrac{3{{a}^{3}}}{8}$.
C. $\dfrac{{{a}^{3}}}{3}$.
D. ${{a}^{3}}$.
Gọi $K$ là trung điểm của $BM\Rightarrow HK\bot BM$.
Gọi $I$ là hình chiếu của $H$ lên $SK$ suy ra $HI\bot \left( SBC \right)$.
Khi đó $HI=\text{d}\left( H,\left( SBC \right) \right)=\dfrac{1}{2}\text{d}\left( A,\left( SBC \right) \right)=\dfrac{\sqrt{15}}{5}a$.
Đặt $AB=x$ suy ra $SH=AM=\dfrac{x\sqrt{3}}{2}$ và $HK=\dfrac{1}{2}AM=\dfrac{x\sqrt{3}}{4}$.
Do đó
$\dfrac{1}{H{{I}^{2}}}=\dfrac{1}{H{{S}^{2}}}+\dfrac{1}{H{{K}^{2}}}\Leftrightarrow \dfrac{1}{{{\left( \dfrac{a\sqrt{15}}{5} \right)}^{2}}}=\dfrac{1}{{{\left( \dfrac{x\sqrt{3}}{2} \right)}^{2}}}+\dfrac{1}{{{\left( \dfrac{x\sqrt{3}}{4} \right)}^{2}}}\Leftrightarrow x=2a$.
Vậy $V=\dfrac{1}{3}\cdot {{S}_{ABC}}\cdot SH=\dfrac{1}{3}\cdot \dfrac{{{x}^{2}}\sqrt{3}}{4}\cdot \dfrac{x\sqrt{3}}{2}=\dfrac{{{x}^{3}}}{8}={{a}^{3}}$.
Đáp án D.