Google
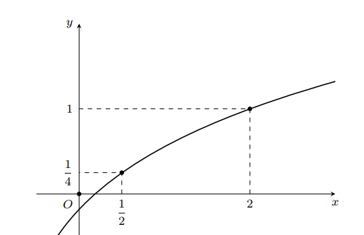
Câu hỏi: Cho hàm số $y=f\left( x \right)$ liên tục và có đạo hàm trên $\left( 0;+\infty \right)$, có đồ thị như hình vẽ đồng thời thỏa mãn ${f}'\left( x \right)-\dfrac{1}{{{x}^{2}}}{f}'\left( \dfrac{1}{x} \right)=\dfrac{5}{18}\left( 1-\dfrac{1}{{{x}^{2}}} \right),\forall x>0$. Diện tích hình phẳng giới hạn bởi các đường $y=\dfrac{f\left( x \right)-{{\left( x-1 \right)}^{2}}}{x}$ và $y=0$ bằng
A. $\dfrac{37}{24}-\dfrac{17}{9}\ln 2$.
B. $\dfrac{37}{24}-\dfrac{11}{9}\ln 2$.
C. $\dfrac{37}{24}-\dfrac{13}{9}\ln 2$.
D. $\dfrac{31}{24}-\dfrac{13}{9}\ln 2$.
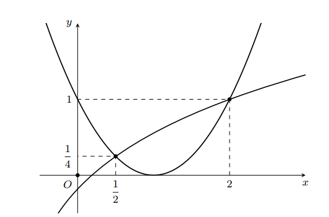Xét phương trình $y=\dfrac{f\left( x \right)-{{\left( x-1 \right)}^{2}}}{x}=0\Leftrightarrow f\left( x \right)={{\left( x-1 \right)}^{2}}\Leftrightarrow \left[ \begin{aligned}
& x=\dfrac{1}{2} \\
& x=2. \\
\end{aligned} \right.$
Khi đó $S=\left| \int\limits_{\dfrac{1}{2}}^{2}{\dfrac{f\left( x \right)-{{\left( x-1 \right)}^{2}}}{x}\text{d}x} \right|=\left| \int\limits_{\dfrac{1}{2}}^{2}{\dfrac{f\left( x \right)}{x}\text{d}x}-\int\limits_{\dfrac{1}{2}}^{2}{\left( x-2+\dfrac{1}{x} \right)\text{d}x} \right|=\left| A-B \right|$.
Tính $B=\int\limits_{\dfrac{1}{2}}^{2}{\left( x-2+\dfrac{1}{x} \right)\text{d}x}=\left. \left( \dfrac{{{x}^{2}}}{2}-2x+\ln x \right) \right|_{\dfrac{1}{2}}^{2}=-\dfrac{9}{8}+2\ln 2$.
Tính $A=\int\limits_{\dfrac{1}{2}}^{2}{\dfrac{f\left( x \right)}{x}\text{d}x}=\int\limits_{\dfrac{1}{2}}^{2}{f\left( x \right)\text{d}\left( \ln x \right)}=\left. f\left( x \right)\ln x \right|_{\dfrac{1}{2}}^{2}-\int\limits_{\dfrac{1}{2}}^{2}{{f}'\left( x \right)\ln x\text{d}x}=\dfrac{5}{4}\ln 2-\int\limits_{\dfrac{1}{2}}^{2}{{f}'\left( x \right)\ln x\text{d}x}$.
Xét phương trình
${f}'\left( x \right)-\dfrac{1}{{{x}^{2}}}{f}'\left( \dfrac{1}{x} \right)=\dfrac{5}{18}\left( 1-\dfrac{1}{{{x}^{2}}} \right),\forall x>0\Leftrightarrow {f}'\left( x \right)\ln x-\dfrac{1}{{{x}^{2}}}{f}'\left( \dfrac{1}{x} \right)\ln x=\dfrac{5}{18}\left( 1-\dfrac{1}{{{x}^{2}}} \right)\ln x$.
Suy ra $\int\limits_{\dfrac{1}{2}}^{2}{{f}'\left( x \right)\ln x\text{d}x}+\int\limits_{\dfrac{1}{2}}^{2}{-\dfrac{1}{{{x}^{2}}}{f}'\left( \dfrac{1}{x} \right)\ln x\text{d}x}=\dfrac{5}{18}\int\limits_{\dfrac{1}{2}}^{2}{\left( 1-\dfrac{1}{{{x}^{2}}} \right)\ln x\text{d}x}$.
Đặt $t=\dfrac{1}{x}\Rightarrow \text{d}t=-\dfrac{1}{{{x}^{2}}}\text{d}x$, ta có $x=\dfrac{1}{2}\Rightarrow t=2$, $x=2\Rightarrow t=\dfrac{1}{2}$.
Khi đó $\int\limits_{\dfrac{1}{2}}^{2}{-\dfrac{1}{{{x}^{2}}}{f}'\left( \dfrac{1}{x} \right)\ln x\text{d}x}=\int\limits_{2}^{\dfrac{1}{2}}{{f}'\left( t \right)\ln \dfrac{1}{t}\text{d}t}=\int\limits_{\dfrac{1}{2}}^{2}{{f}'\left( t \right)\ln t\text{d}t}=\int\limits_{\dfrac{1}{2}}^{2}{{f}'\left( x \right)\ln x\text{d}x}$.
Lại có $\int\limits_{\dfrac{1}{2}}^{2}{\left( 1-\dfrac{1}{{{x}^{2}}} \right)\ln x\text{d}x}=\int\limits_{\dfrac{1}{2}}^{2}{\ln x\text{d}\left( x+\dfrac{1}{x} \right)}=\left. \left( x+\dfrac{1}{x} \right)\ln x \right|_{\dfrac{1}{2}}^{2}-\int\limits_{\dfrac{1}{2}}^{2}{\left( x+\dfrac{1}{x} \right)\dfrac{1}{x}\text{d}x}=5\ln 2-3$.
Suy ra $2\int\limits_{\dfrac{1}{2}}^{2}{{f}'\left( x \right)\ln x\text{d}x}=\dfrac{5}{18}\left( 5\ln 2-3 \right)\Leftrightarrow \int\limits_{\dfrac{1}{2}}^{2}{{f}'\left( x \right)\ln x\text{d}x}=\dfrac{25}{36}\ln 2-\dfrac{5}{12}$.
Do đó $A=\dfrac{5}{4}\ln 2-\left( \dfrac{25}{36}\ln 2-\dfrac{5}{12} \right)=\dfrac{5}{9}\ln 2+\dfrac{5}{12}$.
Vậy $S=\left| A-B \right|=\left| \dfrac{5}{9}\ln 2+\dfrac{5}{12}+\dfrac{9}{8}-2\ln 2 \right|=\dfrac{37}{24}-\dfrac{13}{9}\ln 2$.
B. $\dfrac{37}{24}-\dfrac{11}{9}\ln 2$.
C. $\dfrac{37}{24}-\dfrac{13}{9}\ln 2$.
D. $\dfrac{31}{24}-\dfrac{13}{9}\ln 2$.
& x=\dfrac{1}{2} \\
& x=2. \\
\end{aligned} \right.$
Khi đó $S=\left| \int\limits_{\dfrac{1}{2}}^{2}{\dfrac{f\left( x \right)-{{\left( x-1 \right)}^{2}}}{x}\text{d}x} \right|=\left| \int\limits_{\dfrac{1}{2}}^{2}{\dfrac{f\left( x \right)}{x}\text{d}x}-\int\limits_{\dfrac{1}{2}}^{2}{\left( x-2+\dfrac{1}{x} \right)\text{d}x} \right|=\left| A-B \right|$.
Tính $B=\int\limits_{\dfrac{1}{2}}^{2}{\left( x-2+\dfrac{1}{x} \right)\text{d}x}=\left. \left( \dfrac{{{x}^{2}}}{2}-2x+\ln x \right) \right|_{\dfrac{1}{2}}^{2}=-\dfrac{9}{8}+2\ln 2$.
Tính $A=\int\limits_{\dfrac{1}{2}}^{2}{\dfrac{f\left( x \right)}{x}\text{d}x}=\int\limits_{\dfrac{1}{2}}^{2}{f\left( x \right)\text{d}\left( \ln x \right)}=\left. f\left( x \right)\ln x \right|_{\dfrac{1}{2}}^{2}-\int\limits_{\dfrac{1}{2}}^{2}{{f}'\left( x \right)\ln x\text{d}x}=\dfrac{5}{4}\ln 2-\int\limits_{\dfrac{1}{2}}^{2}{{f}'\left( x \right)\ln x\text{d}x}$.
Xét phương trình
${f}'\left( x \right)-\dfrac{1}{{{x}^{2}}}{f}'\left( \dfrac{1}{x} \right)=\dfrac{5}{18}\left( 1-\dfrac{1}{{{x}^{2}}} \right),\forall x>0\Leftrightarrow {f}'\left( x \right)\ln x-\dfrac{1}{{{x}^{2}}}{f}'\left( \dfrac{1}{x} \right)\ln x=\dfrac{5}{18}\left( 1-\dfrac{1}{{{x}^{2}}} \right)\ln x$.
Suy ra $\int\limits_{\dfrac{1}{2}}^{2}{{f}'\left( x \right)\ln x\text{d}x}+\int\limits_{\dfrac{1}{2}}^{2}{-\dfrac{1}{{{x}^{2}}}{f}'\left( \dfrac{1}{x} \right)\ln x\text{d}x}=\dfrac{5}{18}\int\limits_{\dfrac{1}{2}}^{2}{\left( 1-\dfrac{1}{{{x}^{2}}} \right)\ln x\text{d}x}$.
Đặt $t=\dfrac{1}{x}\Rightarrow \text{d}t=-\dfrac{1}{{{x}^{2}}}\text{d}x$, ta có $x=\dfrac{1}{2}\Rightarrow t=2$, $x=2\Rightarrow t=\dfrac{1}{2}$.
Khi đó $\int\limits_{\dfrac{1}{2}}^{2}{-\dfrac{1}{{{x}^{2}}}{f}'\left( \dfrac{1}{x} \right)\ln x\text{d}x}=\int\limits_{2}^{\dfrac{1}{2}}{{f}'\left( t \right)\ln \dfrac{1}{t}\text{d}t}=\int\limits_{\dfrac{1}{2}}^{2}{{f}'\left( t \right)\ln t\text{d}t}=\int\limits_{\dfrac{1}{2}}^{2}{{f}'\left( x \right)\ln x\text{d}x}$.
Lại có $\int\limits_{\dfrac{1}{2}}^{2}{\left( 1-\dfrac{1}{{{x}^{2}}} \right)\ln x\text{d}x}=\int\limits_{\dfrac{1}{2}}^{2}{\ln x\text{d}\left( x+\dfrac{1}{x} \right)}=\left. \left( x+\dfrac{1}{x} \right)\ln x \right|_{\dfrac{1}{2}}^{2}-\int\limits_{\dfrac{1}{2}}^{2}{\left( x+\dfrac{1}{x} \right)\dfrac{1}{x}\text{d}x}=5\ln 2-3$.
Suy ra $2\int\limits_{\dfrac{1}{2}}^{2}{{f}'\left( x \right)\ln x\text{d}x}=\dfrac{5}{18}\left( 5\ln 2-3 \right)\Leftrightarrow \int\limits_{\dfrac{1}{2}}^{2}{{f}'\left( x \right)\ln x\text{d}x}=\dfrac{25}{36}\ln 2-\dfrac{5}{12}$.
Do đó $A=\dfrac{5}{4}\ln 2-\left( \dfrac{25}{36}\ln 2-\dfrac{5}{12} \right)=\dfrac{5}{9}\ln 2+\dfrac{5}{12}$.
Vậy $S=\left| A-B \right|=\left| \dfrac{5}{9}\ln 2+\dfrac{5}{12}+\dfrac{9}{8}-2\ln 2 \right|=\dfrac{37}{24}-\dfrac{13}{9}\ln 2$.
Đáp án C.