Câu hỏi: Cho hàm số
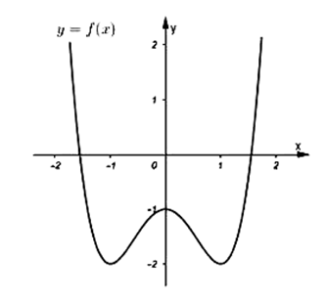
A. 1.
B. 2.
C. 3.
D. 4.

Dựa vào đồ thị ta có:
Khi đó:
Dựa vào đồ thị ta thấy
Suy ra: Phương trình
Ta có:
Suy ra:
Vậy đồ thị hàm số

A. 1.
B. 2.
C. 3.
D. 4.
Dựa vào đồ thị ta có:
Khi đó:
Dựa vào đồ thị ta thấy
Suy ra: Phương trình
Ta có:
Suy ra:
Vậy đồ thị hàm số
Đáp án C.