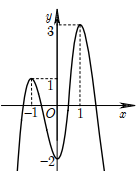
Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}.$ Đồ thị của hàm số $y=f\left( 1-x \right)$ được cho trong hình vẽ bên. Có bao nhiêu...

Cách giải:
Từ đồ thị hàm số $y=f\left( 1-x \right)$ ta suy ra BBT hàm số $y=f\left( x \right)$ như sau:

Đặt $t=\dfrac{1-x}{x+2}=\dfrac{-x+1}{x+2}\Rightarrow t'=\dfrac{-3}{{{\left( x+2 \right)}^{2}}}<0\forall x\ne -2.$
$\Rightarrow $ Với $M$
Ta có BBT hàm số $f\left( t \right)$ như sau:

Khi đó bài toán trở thành: Có bao nhiêu giá trị nguyên của $m$ để phương trình $\left| f\left( t \right)+m \right|=1\left( * \right)$ có đúng 3 nghiệm phân biệt thuộc $\left[ 0;2 \right]?$
Ta có $\left| f\left( t \right)+m \right|=1\Leftrightarrow \left[ \begin{aligned}
& f\left( t \right)+m=1 \\
& f\left( t \right)+m=-1 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& f\left( t \right)=1-m\text{ }\left( 1 \right) \\
& f\left( t \right)=-1-m\text{ }\left( 2 \right) \\
\end{aligned} \right..$
Để (*) có 3 nghiệm phân biệt.
TH1: (1) có 2 nghiệm phân biệt và (2) có 1 nghiệm $\Rightarrow \left\{ \begin{aligned}
& -2<1-m\le 1 \\
& \left[ \begin{aligned}
& 1<-1-m\le 3 \\
& -1-m=-2 \\
\end{aligned} \right. \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& 2\le m<3 \\
& \left[ \begin{aligned}
& -4\le m<-2 \\
& m=1 \\
\end{aligned} \right. \\
\end{aligned} \right.\Rightarrow m=1.$
TH2: (1) có 1 nghiệm và (2) có 2 nghiệm phân biệt $\Rightarrow \left\{ \begin{aligned}
& \left[ \begin{aligned}
& 1<1-m\le 3 \\
& 1-m=-2 \\
\end{aligned} \right. \\
& -2<-1-m\le 1 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& \left[ \begin{aligned}
& -2\le m<0 \\
& m=3 \\
\end{aligned} \right. \\
& -2\le m<1 \\
\end{aligned} \right.\Rightarrow -2\le m<0.$
$\Rightarrow m\in \left[ -2;0 \right)\cup \left\{ 1 \right\}.$ Mà $m\in \mathbb{Z}\Rightarrow m\in \left\{ -2;-1;1 \right\}.$
Vậy có 3 giá trị của $m$ thỏa mãn.