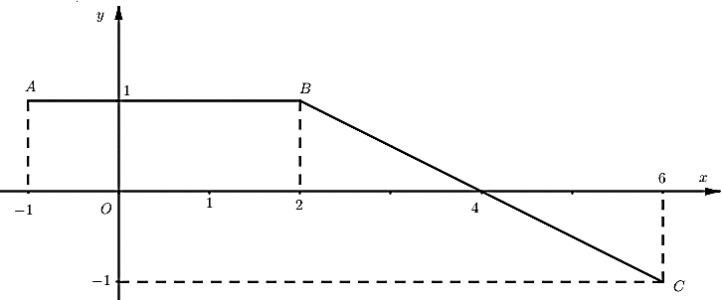
Câu hỏi: Cho hàm số $y=f\left( x \right)$ liên tục trên đoạn $\left[ -1;6 \right]$ và có đồ thị là đường gấp khúc $ABC$ trong hình bên. Biết $F$ là nguyên hàm của $f$ thỏa mãn $F\left( -1 \right)=-1$. Giá trị của $F\left( 4 \right)+F\left( 6 \right)$ bằng
A. $10$.
B. $5$.
C. $6$.
D. $7$.
A. $10$.
B. $5$.
C. $6$.
D. $7$.
Từ đồ thị của hàm số ta xác định được $f\left( x \right)=\left\{ \begin{aligned}
& 1\text{ khi }-1\le x<2 \\
& -\dfrac{1}{2}x+2\text{ khi }2\le x\le 6 \\
\end{aligned} \right.$.
Do $F$ là nguyên hàm của $f$ nên $F\left( x \right)=\left\{ \begin{aligned}
& x+{{C}_{1}}\text{ khi }-1\le x<2 \\
& -\dfrac{1}{4}{{x}^{2}}+2x+{{C}_{2}}\text{ khi }2\le x\le 6 \\
\end{aligned} \right.$.
Ta có $F\left( -1 \right)=-1\Leftrightarrow -1+{{C}_{1}}=-1\Leftrightarrow {{C}_{1}}=0$.
Hàm số $y=f\left( x \right)$ liên tục trên đoạn $\left[ -1;6 \right]$ $\Rightarrow F\left( x \right)$ liên tục trên đoạn $\left[ -1;6 \right]$
$\Rightarrow F\left( x \right)$ liên tục tại $x=2$ $\Rightarrow \underset{x\to {{2}^{-}}}{\mathop{\lim }} F\left( x \right)=\underset{x\to {{2}^{+}}}{\mathop{\lim }} F\left( x \right)\Leftrightarrow 2+{{C}_{1}}=3+{{C}_{2}}\Leftrightarrow {{C}_{2}}=-1.$
Suy ra $F\left( x \right)=\left\{ \begin{aligned}
& x+{{C}_{1}}\text{ khi }-1\le x<2 \\
& -\dfrac{1}{4}{{x}^{2}}+2x-1\text{ khi }2\le x\le 6 \\
\end{aligned} \right. $. Vậy $ F\left( 4 \right)+F\left( 6 \right)=5$.
& 1\text{ khi }-1\le x<2 \\
& -\dfrac{1}{2}x+2\text{ khi }2\le x\le 6 \\
\end{aligned} \right.$.
Do $F$ là nguyên hàm của $f$ nên $F\left( x \right)=\left\{ \begin{aligned}
& x+{{C}_{1}}\text{ khi }-1\le x<2 \\
& -\dfrac{1}{4}{{x}^{2}}+2x+{{C}_{2}}\text{ khi }2\le x\le 6 \\
\end{aligned} \right.$.
Ta có $F\left( -1 \right)=-1\Leftrightarrow -1+{{C}_{1}}=-1\Leftrightarrow {{C}_{1}}=0$.
Hàm số $y=f\left( x \right)$ liên tục trên đoạn $\left[ -1;6 \right]$ $\Rightarrow F\left( x \right)$ liên tục trên đoạn $\left[ -1;6 \right]$
$\Rightarrow F\left( x \right)$ liên tục tại $x=2$ $\Rightarrow \underset{x\to {{2}^{-}}}{\mathop{\lim }} F\left( x \right)=\underset{x\to {{2}^{+}}}{\mathop{\lim }} F\left( x \right)\Leftrightarrow 2+{{C}_{1}}=3+{{C}_{2}}\Leftrightarrow {{C}_{2}}=-1.$
Suy ra $F\left( x \right)=\left\{ \begin{aligned}
& x+{{C}_{1}}\text{ khi }-1\le x<2 \\
& -\dfrac{1}{4}{{x}^{2}}+2x-1\text{ khi }2\le x\le 6 \\
\end{aligned} \right. $. Vậy $ F\left( 4 \right)+F\left( 6 \right)=5$.
Đáp án B.