Câu hỏi: Cho hàm số $y=f\left( x \right)$ là hàm đa thức bậc bốn, có đồ thị ${f}'\left( x \right)$ như hình vẽ
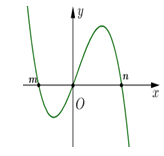
Phương trình $f\left( x \right)=0$ có 4 nghiệm phân biệt khi và chỉ khi
A. $f\left( 0 \right)>0$
B. $f\left( 0 \right)<0<f\left( m \right)$.
C. $f\left( m \right)<0<f\left( n \right)$.
D. $f\left( 0 \right)<0<f\left( n \right)$.

Phương trình $f\left( x \right)=0$ có 4 nghiệm phân biệt khi và chỉ khi
A. $f\left( 0 \right)>0$
B. $f\left( 0 \right)<0<f\left( m \right)$.
C. $f\left( m \right)<0<f\left( n \right)$.
D. $f\left( 0 \right)<0<f\left( n \right)$.
Ta có ${f}'\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& x=m \\
& x=0 \\
& x=n \\
\end{aligned} \right.$. Khi đó ta có bảng biến thiên

Ta có $\int\limits_{m}^{0}{\left| {f}'\left( x \right) \right|}dx<\int\limits_{0}^{n}{\left| {f}'\left( x \right) \right|}dx\Leftrightarrow f\left( m \right)-f\left( 0 \right)<f\left( n \right)-f\left( 0 \right)\Leftrightarrow f\left( m \right)<f\left( n \right)$.
Dựa vào bảng biến thiên để phương trình $f\left( x \right)=0$ có 4 nghiệm thì $f\left( 0 \right)<0<f\left( m \right)$.
& x=m \\
& x=0 \\
& x=n \\
\end{aligned} \right.$. Khi đó ta có bảng biến thiên
Ta có $\int\limits_{m}^{0}{\left| {f}'\left( x \right) \right|}dx<\int\limits_{0}^{n}{\left| {f}'\left( x \right) \right|}dx\Leftrightarrow f\left( m \right)-f\left( 0 \right)<f\left( n \right)-f\left( 0 \right)\Leftrightarrow f\left( m \right)<f\left( n \right)$.
Dựa vào bảng biến thiên để phương trình $f\left( x \right)=0$ có 4 nghiệm thì $f\left( 0 \right)<0<f\left( m \right)$.
Đáp án B.