Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau: 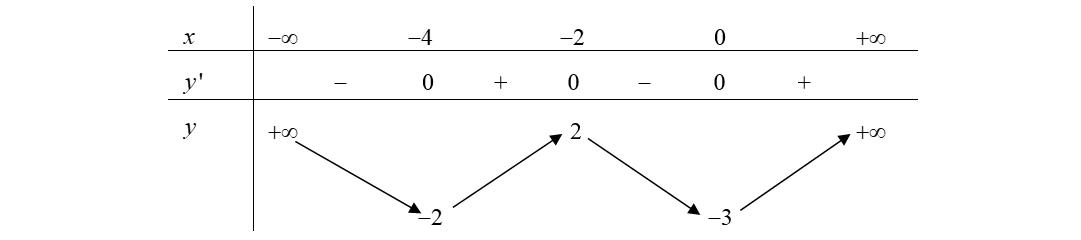Số giá trị nguyên của tham số $m$ để phương trình $3f\left( {{x}^{2}}-4x \right)=m+5$...

Phương pháp:
- Đặt $t={{x}^{2}}-4x,$ với $x\in \left( 0;+\infty \right),$ đưa phương trình về dạng $f\left( t \right)=m\left( * \right).$
- Xác định mỗi nghiệm $t$ cho bao nhiêu nghiệm $x$ trên từng khoảng cụ thể.
- Tìm điều kiện về số nghiệm của phương trình (*) để phương trình ban đầu có ít nhất 5 nghiệm phân biệt.
Cách giải:
Đặt $t={{x}^{2}}-4x,$ với $x\in \left( 0;+\infty \right),$ khi đó phương trình trở thành $3f\left( t \right)=m+5\Leftrightarrow f\left( t \right)=\dfrac{m+5}{3}\left( * \right).$
Ta có $t'\left( x \right)=2x-4=0\Leftrightarrow x=2\in \left( 0;+\infty \right).$
BBT:

Dựa vào BBT đề bài cho, ta thấy phương trình $f\left( t \right)=\dfrac{m+5}{3}$ có tối đa 4 nghiệm, mỗi nghiệm $t\in \left( -4;0 \right)$ cho 2 nghiệm $x$ phân biệt, mỗi nghiệm $t\in \left[ 0;+\infty \right)\cup \left\{ -4 \right\}$ cho 1 nghiệm $x.$
Để phương trình ban đầu có ít nhất 5 nghiệm thuộc $\left( 0;+\infty \right)$ thì phương trình (*):
TH1: Có 1 nghiệm $t\in \left( -4;0 \right)$ và 3 nghiệm $t\in \left[ 0;+\infty \right)\cup \left\{ -4 \right\}$ (ktm).
TH2: Có 2 nghiệm $t\in \left( -4;0 \right)$ và 1 nghiệm $t\in \left[ 0;+\infty \right)\cup \left\{ -4 \right\}$ (ktm).
$\Rightarrow \left\{ \begin{aligned}
& -2<\dfrac{m+5}{3}\le 2 \\
& -3\le \dfrac{m+5}{3}\ne -2 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& -6<m+5\le 5 \\
& -9\le m+5\ne -6 \\
\end{aligned} \right.$
$\Leftrightarrow \left\{ \begin{aligned}
& -11<m\le 0 \\
& -14\le m\ne -11 \\
\end{aligned} \right.\Leftrightarrow m\in \left[ -14;0 \right]\backslash \left\{ -11 \right\}$.
Mà $m\in \mathbb{Z}\Rightarrow $ Có 14 giá trị của $m$ thỏa mãn yêu cầu bài toán.