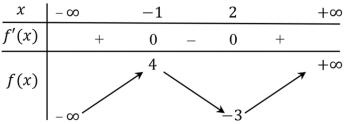
Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau: Điểm cực tiểu của hàm số $y=f\left( 3x \right)$ là

Phương pháp:
- Tính đạo hàm của hàm số $y=f\left( 3x \right).$
- Giải phương trình $y'=0.$
- Lập BXD $y'$ và xác định điểm cực tiểu của hàm số là điểm mà tại đó hàm số liên tục và qua đó đạo hàm đổi dấu từ âm sang dương.
Cách giải:
Ta có $y=f\left( 3x \right)\Rightarrow y'=3.f'\left( 3x \right).$
Cho $y'=0\Leftrightarrow \left[ \begin{aligned}
& 3x=-1 \\
& 3x=2 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=-\dfrac{1}{3} \\
& x=\dfrac{2}{3} \\
\end{aligned} \right..$
Bảng xét dấu:

Dựa vào bảng xét dấu ta thấy điểm cực tiểu của hàm số là $x=\dfrac{2}{3}.$