Google
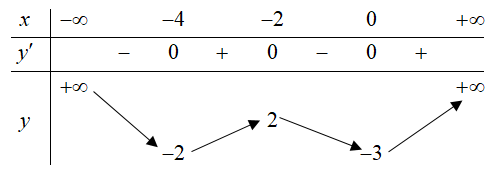
Câu hỏi: Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau
Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $6f\left( {{x}^{2}}-4x \right)=m$ có ít nhất $3$ nghiệm thực phân biệt thuộc khoảng $\left( 0;+\infty \right)$ ?
A. $29$.
B. $25$.
C. $24$.
D. $30$.
A. $29$.
B. $25$.
C. $24$.
D. $30$.
Ta có: $6f\left( {{x}^{2}}-4x \right)=m\Leftrightarrow f\left( {{x}^{2}}-4x \right)=\dfrac{m}{6}$
Đặt $u={{x}^{2}}-4x\Rightarrow {u}'=0\Leftrightarrow x=2$.
Để phương trình $f\left( {{x}^{2}}-4x \right)=\dfrac{m}{6}$ có ít nhất 3 nghiệm phân biệt thuộc $\left( 0;+\infty \right)$ :
$\Leftrightarrow -3<\dfrac{m}{6}\le 2\Leftrightarrow -18<m\le 12$.
Đặt $u={{x}^{2}}-4x\Rightarrow {u}'=0\Leftrightarrow x=2$.
$\Leftrightarrow -3<\dfrac{m}{6}\le 2\Leftrightarrow -18<m\le 12$.
Đáp án D.