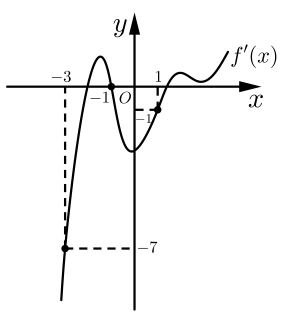
Cho hàm số $f(x)$, đồ thị của hàm số $y={f}'(x)$ là đường cong trong hình vẽ bên dưới. Giá trị lớn nhất của hàm số...

Ta có $g'\left( x \right)=24f'\left( 2x \right)+96{{x}^{2}}+24x-12=12\left[ 2f'\left( 2x \right)+8{{x}^{2}}+2x-1 \right]$
$g'\left( x \right)=0\Leftrightarrow 12\left[ 2f'\left( 2x \right)+8{{x}^{2}}+2x-1 \right]=0\Leftrightarrow 2f'\left( 2x \right)+8{{x}^{2}}+2x-1=0\left( * \right)$
Đặt $t=2x,x\in \left[ -\dfrac{3}{2};\dfrac{1}{2} \right]\Rightarrow t\in \left[ -3;1 \right].$
Khi đó phương trình $\left( * \right)$ trở thành phương trình sau:
$2f'\left( t \right)+2{{t}^{2}}+t-1=0\Leftrightarrow f'\left( t \right)=-{{t}^{2}}-\dfrac{1}{2}t+\dfrac{1}{2}\left( ** \right)$
Ta có đồ thị như sau:

$f'\left( t \right)=0\Leftrightarrow \left[ \begin{aligned}
& t=-3 \\
& t=-1 \\
& t=1 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=-\dfrac{3}{2} \\
& x=-\dfrac{1}{2} \\
& x=\dfrac{1}{2} \\
\end{aligned} \right.$
Ta có bảng biến thiên như sau:

Dựa vào bảng biến thiên và đồ thị hàm số ta có giá trị lớn nhất của hàm số $g\left( x \right)$ đạt tại $x=-\dfrac{1}{2}\Rightarrow g\left( -\dfrac{1}{2} \right)=12f\left( -1 \right)+2026.$