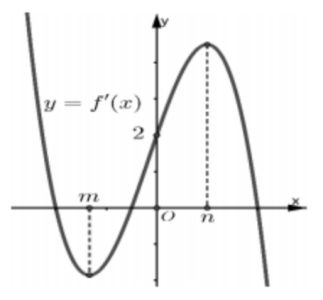
Câu hỏi: Cho hàm số $f\left( x \right)=a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+dx+e,\left( a\ne 0 \right)$ có đồ thị của đạo hàm $f'\left( x \right)$ như hình vẽ. Biết rằng $e>n.$
Số điểm cực trị của hàm số $y=f'\left( f\left( x \right)-2x \right)$ là
A. 7.
B. 6.
C. 10.
D. 14.

Số điểm cực trị của hàm số $y=f'\left( f\left( x \right)-2x \right)$ là
A. 7.
B. 6.
C. 10.
D. 14.
Ta có: $y'=\left( f'\left( x \right)-2 \right)f''\left[ f\left( x \right)-2x \right]$
$y'=0\Leftrightarrow \left( f'\left( x \right)-2 \right)f''\left[ f\left( x \right)-2x \right]=0\Leftrightarrow \left[ \begin{aligned}
& f'\left( x \right)-2=0\text{ }\left( 1 \right) \\
& f''\left[ f\left( x \right)-2x \right]=0\left( 2 \right) \\
\end{aligned} \right.$
Xét phương trình $\left( 1 \right)\Leftrightarrow f'\left( x \right)=2.$

Từ đồ thị ta có phương trình $\left( 1 \right)$ có 3 nghiệm phân biệt ${{x}_{1}},0,{{x}_{2}}\left( {{x}_{1}}<m<0<n<{{x}_{2}} \right).$
Xét phương trình $\left( 2 \right).$
Trước hết ta có: $f'\left( x \right)=4a{{x}^{3}}+3b{{x}^{2}}+2cx+d.$
$f'\left( 0 \right)=2\Leftrightarrow d=2.$
Suy ra: $f\left( x \right)=a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+2x+e.$
$\left( 2 \right)\Leftrightarrow f''\left[ f\left( x \right)-2x \right]=0\Leftrightarrow \left[ \begin{aligned}
& f\left( x \right)-2x=m \\
& f\left( x \right)-2x=n \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+e=m \\
& a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+e=n \\
\end{aligned} \right.$
$\Leftrightarrow \left[ \begin{aligned}
& a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}=m-e\left( 2a \right) \\
& a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}=n-e\text{ }\left( 2b \right) \\
\end{aligned} \right..$
Số nghiệm của hai phương trình $\left( 2a \right)$ và $\left( 2b \right)$ lần lượt bằng số giao điểm của hai đường thẳng $y=m-e$ và $y=n-e$ (trong đó $m-e<n-e<0)$ với đồ thị hàm số $g\left( x \right)=a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}.$
$g'\left( x \right)=4a{{x}^{3}}+3b{{x}^{2}}+2cx.$
$g'\left( x \right)=0\Leftrightarrow 4a{{x}^{3}}+3b{{x}^{2}}+2cx=0\Leftrightarrow 4a{{x}^{3}}+3b{{x}^{3}}+2cx+2=2$
$\Leftrightarrow f'\left( x \right)=2\Leftrightarrow \left[ \begin{aligned}
& x={{x}_{1}}<0 \\
& x=0 \\
& x={{x}_{2}}>0 \\
\end{aligned} \right.$
Từ đồ thị hàm số $y=f'\left( x \right)$ suy ra:
+) $\underset{x\Rightarrow -\infty }{\mathop{\lim }} f'\left( x \right)=+\infty $ nên $a<0$ nên $\underset{x\Rightarrow -\infty }{\mathop{\lim }} g\left( x \right)=-\infty ,\underset{x\Rightarrow +\infty }{\mathop{\lim }} g\left( x \right)=-\infty .$
Bảng biến thiên của hàm số $y=g\left( x \right):$

Từ bảng biến thiên suy ra hai phương trình $\left( 2a \right),\left( 2b \right)$ mỗi phương trình có hai nghiệm phân biệt
(hai phương trình không có nghiệm trùng nhau) và khác ${{x}_{1}},0,{{x}_{2}}.$
Suy ra phương trình $\left( f'\left( x \right)-2 \right)f''\left[ f\left( x \right)-2x \right]=0$ có 7 nghiệm đơn phân biệt. Vậy hàm số $y=f'\left[ f\left( x \right)-2x \right]$ có 7 điểm cực trị.
$y'=0\Leftrightarrow \left( f'\left( x \right)-2 \right)f''\left[ f\left( x \right)-2x \right]=0\Leftrightarrow \left[ \begin{aligned}
& f'\left( x \right)-2=0\text{ }\left( 1 \right) \\
& f''\left[ f\left( x \right)-2x \right]=0\left( 2 \right) \\
\end{aligned} \right.$
Xét phương trình $\left( 1 \right)\Leftrightarrow f'\left( x \right)=2.$
Từ đồ thị ta có phương trình $\left( 1 \right)$ có 3 nghiệm phân biệt ${{x}_{1}},0,{{x}_{2}}\left( {{x}_{1}}<m<0<n<{{x}_{2}} \right).$
Xét phương trình $\left( 2 \right).$
Trước hết ta có: $f'\left( x \right)=4a{{x}^{3}}+3b{{x}^{2}}+2cx+d.$
$f'\left( 0 \right)=2\Leftrightarrow d=2.$
Suy ra: $f\left( x \right)=a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+2x+e.$
$\left( 2 \right)\Leftrightarrow f''\left[ f\left( x \right)-2x \right]=0\Leftrightarrow \left[ \begin{aligned}
& f\left( x \right)-2x=m \\
& f\left( x \right)-2x=n \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+e=m \\
& a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+e=n \\
\end{aligned} \right.$
$\Leftrightarrow \left[ \begin{aligned}
& a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}=m-e\left( 2a \right) \\
& a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}=n-e\text{ }\left( 2b \right) \\
\end{aligned} \right..$
Số nghiệm của hai phương trình $\left( 2a \right)$ và $\left( 2b \right)$ lần lượt bằng số giao điểm của hai đường thẳng $y=m-e$ và $y=n-e$ (trong đó $m-e<n-e<0)$ với đồ thị hàm số $g\left( x \right)=a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}.$
$g'\left( x \right)=4a{{x}^{3}}+3b{{x}^{2}}+2cx.$
$g'\left( x \right)=0\Leftrightarrow 4a{{x}^{3}}+3b{{x}^{2}}+2cx=0\Leftrightarrow 4a{{x}^{3}}+3b{{x}^{3}}+2cx+2=2$
$\Leftrightarrow f'\left( x \right)=2\Leftrightarrow \left[ \begin{aligned}
& x={{x}_{1}}<0 \\
& x=0 \\
& x={{x}_{2}}>0 \\
\end{aligned} \right.$
Từ đồ thị hàm số $y=f'\left( x \right)$ suy ra:
+) $\underset{x\Rightarrow -\infty }{\mathop{\lim }} f'\left( x \right)=+\infty $ nên $a<0$ nên $\underset{x\Rightarrow -\infty }{\mathop{\lim }} g\left( x \right)=-\infty ,\underset{x\Rightarrow +\infty }{\mathop{\lim }} g\left( x \right)=-\infty .$
Bảng biến thiên của hàm số $y=g\left( x \right):$
Từ bảng biến thiên suy ra hai phương trình $\left( 2a \right),\left( 2b \right)$ mỗi phương trình có hai nghiệm phân biệt
(hai phương trình không có nghiệm trùng nhau) và khác ${{x}_{1}},0,{{x}_{2}}.$
Suy ra phương trình $\left( f'\left( x \right)-2 \right)f''\left[ f\left( x \right)-2x \right]=0$ có 7 nghiệm đơn phân biệt. Vậy hàm số $y=f'\left[ f\left( x \right)-2x \right]$ có 7 điểm cực trị.
Đáp án A.