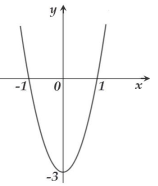
Cho hàm số $f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có đồ thị $\left( C \right)$ tiếp xúc với đường thẳng $y=4$ tại điểm có hoành độ dương...

Phương pháp:
- Dựa vào đồ thị tìm hàm số $f'\left( x \right).$
- Dựa vào $f\left( x \right)$ tính $f'\left( x \right),$ đồng nhất hệ số tìm $a,b,c.$
- Đồ thị hàm số $y=f\left( x \right)$ và $y=g\left( x \right)$ tiếp xúc với nhau khi hệ $\left\{ \begin{aligned}
& f\left( x \right)=g\left( x \right) \\
& f'\left( x \right)=g'\left( x \right) \\
\end{aligned} \right. $ có nghiệm, giải hệ tìm hoành độ điểm tiếp xúc và tìm hàm số $ f\left( x \right)$ tường minh.
- Xét hàm số $f\left( x \right)$ trên $\left[ 0;2 \right],$ tìm $\underset{\left[ 0;2 \right]}{\mathop{\min }} f\left( x \right),\underset{\left[ 0;2 \right]}{\mathop{\max }} f\left( x \right)$.
- Kết luận $\underset{\left[ 0;2 \right]}{\mathop{\max }} \left| f\left( x \right) \right|=\max \left\{ \left| \underset{\left[ 0;2 \right]}{\mathop{\min }} f\left( x \right) \right|,\left| \underset{\left[ 0;2 \right]}{\mathop{\max }} f\left( x \right) \right| \right\}.$
Cách giải:
Dựa vào hình vẽ ta thấy: Phương trình $f'\left( x \right)=0$ có 2 nghiệm phân biệt $x=\pm 1$ nên có dạng $f'\left( x \right)=k\left( x-1 \right)\left( x+1 \right).$
Lại có đồ thị hàm số đi qua điểm có tọa độ $\left( 0;-3 \right)\Rightarrow k=3.$
Suy ra $f'\left( x \right)=3\left( x-1 \right)\left( x+1 \right)=3{{x}^{3}}-3.$
Mà $f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d\Rightarrow f'\left( x \right)=3a{{x}^{2}}+2bx+c.$
Đồng nhất hệ số ta có: $\left\{ \begin{aligned}
& 3a=3 \\
& 2b=0 \\
& c=-3 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& a=1 \\
& b=0 \\
& c=-3 \\
\end{aligned} \right.\Rightarrow f\left( x \right)={{x}^{3}}-3x+d.$
Theo bài ra ta có: Đồ thị hàm số $f\left( x \right)={{x}^{3}}-3x+d$ tiếp xúc với đường $y=4$ tại điểm có hoành độ dương nên $\left\{ \begin{aligned}
& {{x}^{3}}-3x+d=4 \\
& 3{{x}^{3}}-3=0 \\
& x>0 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& x=1 \\
& d=6 \\
\end{aligned} \right.\Rightarrow f\left( x \right)={{x}^{3}}-3x+6.$
Xét hàm số $f\left( x \right)={{x}^{3}}-3x+6$ trên $\left[ 0;2 \right]$ ta có $f'\left( x \right)=3{{x}^{2}}-3=0\Leftrightarrow \left[ \begin{aligned}
& x=1\in \left[ 0;2 \right] \\
& x=-1\notin \left[ 0;2 \right] \\
\end{aligned} \right..$
$f\left( 0 \right)=6,f\left( 1 \right)=4,f\left( 2 \right)=8.$
$\Rightarrow \underset{\left[ 0;2 \right]}{\mathop{\min }} f\left( x \right)=f\left( 1 \right)=4,\underset{\left[ 0;2 \right]}{\mathop{\max }} f\left( x \right)=f\left( 2 \right)=8.$
Vậy $\underset{\left[ 0;2 \right]}{\mathop{\max }} \left| f\left( x \right) \right|=\max \left\{ \left| \underset{\left[ 0;2 \right]}{\mathop{\min }} f\left( x \right) \right|,\left| \underset{\left[ 0;2 \right]}{\mathop{\max }} f\left( x \right) \right| \right\}=8.$