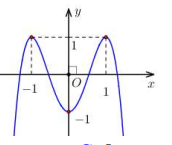
Cho hàm số bậc bốn ${y=f(x)}$ có đồ thị là đường cong trong hình...

Nhìn vào đồ thị ta thấy ${f(x)=0}$ có 4 nghiệm phân biệt theo thứ tự ${a, b, c, d}$.
${
\text { Ta có: } f(f(x))=0 \Leftrightarrow\left[\begin{array}{l}
f(x)=a, a \in(-\infty ;-1) \\
f(x)=b, b \in(-1 ; 0) \\
f(x)=c, c \in(0 ; 1) \\
f(x)=d, d \in(1 ;+\infty)
\end{array} .\right.
}$

Dựa vào đồ thị ta thấy:
Phương trình ${f(x)=a}$ có 2 nghiệm thực phân biệt.
Phương trình ${f(x)=b}$ có 4 nghiệm thực phân biệt.
Phương trình ${f(x)=c}$ có 4 nghiệm thực phân biệt.
Phương trình ${f(x)=d}$ vô nghiệm trên ${\mathbb{R}}$.
Vậy phương trình ${f(f(x))=0}$ có 10 nghiệm thực phân biệt.