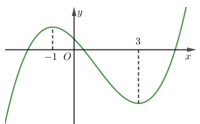
Cho hàm số bậc ba $y=f\left( x \right)$ có đồ thị như hình vẽ: Gọi $S$ là tập hợp tất cả các giá trị nguyên của tham số $m$ để hàm số $y=f\left(...

Phương pháp:
- Tính $y',$ sử dụng tương giao giải phương trình $y'=0.$
- Hàm số có 3 điểm cực trị khi $y'=0$ có 3 nghiệm phân biệt.
- Xét các TH có thể xảy ra và tìm $m.$
Cách giải:
Ta có $y=f\left( {{\left( x-1 \right)}^{2}}+m \right)\Rightarrow y'=2\left( x-1 \right)f'\left( {{\left( x-1 \right)}^{2}}+m \right)=0$
$\Rightarrow \left[ \begin{aligned}
& x=1 \\
& f'\left( {{\left( x-1 \right)}^{2}}+m \right)=0 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=1 \\
& {{\left( x-1 \right)}^{2}}+m=-1 \\
& {{\left( x-1 \right)}^{2}}+m=-3 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=1 \\
& {{\left( x-1 \right)}^{2}}=-m-1\left( 1 \right) \\
& {{\left( x-1 \right)}^{2}}=-m+3\left( 2 \right) \\
\end{aligned} \right.$
Hàm số có 3 điểm cực trị khi $y'=0$ có 3 nghiệm phân biệt.
+ TH1: (1) có nghiệm kép $x=1$ hoặc vô nghiệm và (2) có 2 nghiệm phân biệt khác 1
$\Rightarrow \left\{ \begin{aligned}
& -m-1\le 0 \\
& -m+3>0 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& m\ge -1 \\
& m<3 \\
\end{aligned} \right.\Leftrightarrow -1\le m<3.$
+ TH2: (2) có nghiệm kép $x=1$ và (2) có 1 nghiệm phân biệt khác 1
$\Rightarrow \left\{ \begin{aligned}
& -m-1>0 \\
& -m+3\le 0 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& m<-1 \\
& m\ge 3 \\
\end{aligned} \right.\Leftrightarrow m\in \varnothing .$
Suy ra $-1\le m<3\Rightarrow S=\left\{ -1;0;1;2 \right\}.$
Vậy tổng các phần tử của $S$ là: $-1+0+1+2=2.$