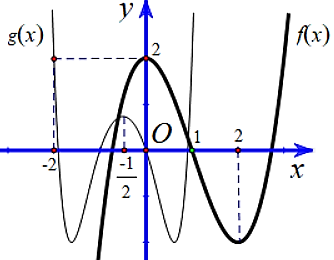
Cho hàm số bậc ba $y=f\left( x \right)$ có đồ thị là đường cong...

Hàm số $f\left( x \right)=m{{x}^{3}}+n{{x}^{2}}+px+q$
${f}'\left( x \right)=3m{{x}^{2}}+2nx+p$
Hàm số $f\left( x \right)$ có hai điểm cực trị $x=0$ ; $x=2$ nên $\left\{ \begin{aligned}
& {f}'\left( 0 \right)=0 \\
& {f}'\left( 2 \right)=0 \\
\end{aligned} \right.$
Suy ra, $\left\{ \begin{aligned}
& p=0 \\
& 12m+4n=0 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& p=0 \\
& n=-3m \\
\end{aligned} \right.$
Do đó, $f\left( x \right)=m{{x}^{3}}-3m{{x}^{2}}+q$
Từ đồ thị $f\left( x \right)$ ta có $\left\{ \begin{aligned}
& f\left( \text{1} \right)=0 \\
& f\left( \text{0} \right)=\text{2} \\
\end{aligned} \right.$$\Rightarrow \left\{ \begin{aligned}
& -2m+q=0 \\
& q=2 \\
\end{aligned} \right.$$\Leftrightarrow $ $ \left\{ \begin{aligned}
& m=1 \\
& q=2 \\
\end{aligned} \right.$
Vậy $f\left( x \right)={{x}^{3}}-3{{x}^{2}}+2$.
Ta có $g\left( 0 \right)=0$ $\Rightarrow $ $f\left( c \right)={{c}^{3}}-3{{c}^{2}}+2=0$ $\Leftrightarrow \left[ \begin{aligned}
& c=1 \\
& c=1\pm \sqrt{3} \\
\end{aligned} \right.$
Do $c\in \mathbb{Q}$ nên chọn $c=1$.
Đồ thị hàm số $g\left( x \right)$ nhận đường thẳng $x=-\dfrac{1}{2}$ làm trục đối xứng nên $g\left( -1 \right)=g\left( 0 \right)=0$
Từ $g\left( -1 \right)=0$ $\Rightarrow f\left( a-b+1 \right)=0$ $\Rightarrow $ ${{\left( a-b+1 \right)}^{3}}-3{{\left( a-b+1 \right)}^{2}}+2=0$ $\Leftrightarrow \left[ \begin{aligned}
& a-b+1=1 \\
& a-b+1=1\pm \sqrt{3} \\
\end{aligned} \right.$.
Do $a,b\in \mathbb{Q}$ nên chọn $a-b=0\Leftrightarrow a=b$
Suy ra $a{{x}^{2}}+bx+c=a{{x}^{2}}+ax+1$.
Có $g\left( -2 \right)=2\Rightarrow f\left( 2a+1 \right)=2$ $\Rightarrow {{\left( 2a+1 \right)}^{3}}-3{{\left( 2a+1 \right)}^{2}}+2=2$ $\Leftrightarrow \left[ \begin{aligned}
& 2a+1=0 \\
& 2a+1=3 \\
\end{aligned} \right.$
$\Rightarrow \left[ \begin{aligned}
& a=-\dfrac{1}{2} \\
& a=1 \\
\end{aligned} \right.$.
Từ đồ thị hàm số $f\left( x \right)$ và $g\left( x \right)$ suy ra: $\underset{x\to +\infty }{\mathop{\lim }} f\left( x \right)=+\infty $ và $\underset{x\to +\infty }{\mathop{\lim }} g\left( x \right)=+\infty $.
Vậy chọn $a=1$.
Khi đó, $g\left( x \right)=f\left( a{{x}^{2}}+bx+c \right)=f\left( {{x}^{2}}+x+1 \right)$.
Xét hàm số $g\left( x \right)$ trên đoạn $\left[ -2;2 \right]$
Đặt $u={{x}^{2}}+x+1$.
${u}'\left( x \right)=2x+1=0$ $\Leftrightarrow x=-\dfrac{1}{2}\in \left[ -2;2 \right]$.
$u\left( -\dfrac{1}{2} \right)=\dfrac{3}{4}$ ; $u\left( -\text{2} \right)=\text{3}$ ; $u\left( 2 \right)=7$ $\Rightarrow $ $u\in \left[ \dfrac{3}{\text{4}};7 \right]$
Vậy $\underset{\left[ -2;2 \right]}{\mathop{Max}} g\left( x \right)=\underset{\left[ \dfrac{3}{4};7 \right]}{\mathop{Max}} f\left( u \right)=f\left( 7 \right)=198$.