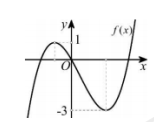
Cho hàm số bậc ba $f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có đồ thị như hình vẽ sau. Có bao nhiêu số dương trong các số $a,b,c,d?$

Phương pháp:
- Sử dụng chiều đồ thị suy ra dấu của hệ số $a.$
- Dựa vào giao điểm của đồ thị với trục tung suy ra dấu của hệ số $d.$
- Dựa vào dấu các điểm cực trị của hàm số suy ra dấu của hệ số $b,c.$
Cách giải:
Đồ thị hàm số có nhánh cuối cùng đi lên nên $a>0.$
Đồ thị đi qua điểm $O\left( 0;0 \right)$ nên $d=0.$
Hàm số có 2 điểm cực trị ${{x}_{1}},{{x}_{2}}$ và $\left\{ \begin{aligned}
& {{x}_{1}}+{{x}_{2}}>0 \\
& {{x}_{1}}.{{x}_{2}}<0 \\
\end{aligned} \right..$
Ta có $y'=3a{{x}^{2}}+2bx+c$ có 2 nghiệm phân biệt ${{x}_{1}},{{x}_{2}}$ thỏa mãn $\left\{ \begin{aligned}
& {{x}_{1}}+{{x}_{2}}>0 \\
& {{x}_{1}}.{{x}_{2}}<0 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& \dfrac{-2b}{3a}>0 \\
& \dfrac{c}{3a}<0 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& b<0 \\
& c<0 \\
\end{aligned} \right..$
Vậy có một số dương trong các số $a,b,c,d.$