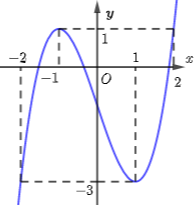
Cho hàm số bậc ba $f=f\left( x \right)$ có đồ thị như hình vẽ. Có...

Gọi $a,b,c$ là hoành độ giao điểm của đồ thị hàm số $y=f\left( x \right)$ và trục hoành.
Dựa vào đồ thị ta có:
$f(x)=0 \Leftrightarrow\left[\begin{array}{l}
x=a(-2<a<-1) \\
x=b(-1<a<0) \\
x=c(1<a<2)
\end{array}\right.$
$f(f(x)-m)=0 \Leftrightarrow\left[\begin{array}{l}f(x)-m=a \\ f(x)-m=b \\ f(x)-m=c\end{array} \Leftrightarrow\left[\begin{array}{l}f(x)=m+a(1) \\ f(x)=m+b(2) \\ f(x)=m+c(3)\end{array}\right.\right.$
Phương trình (1) có 3 nghiệm phân biệt khi $-3<m+a<1$, mà $1<-a<2$ ; suy ra $-2<m<3$.
Phương trình (2) có 3 nghiệm phân biệt khi $-3<m+b<1$, mà $0<-b<1$ ; suy ra $-3<m<2$.
Phương trình (3) có 3 nghiệm phân biệt khi $-3<m+c<1$, mà $-2<-c<-1$ ; suy ra $-5<m<0$.
Do đó để phương trình đã̃ cho có tất cả 9 nghiệm thực phân biệt thì $\left\{\begin{array}{l}-2<m<3 \\ -3<m<2 \\ -5<m<0\end{array} \Rightarrow-2<m<0\right.$.
Mà $m \in \mathbb{Z}$, nên $m=-1$.