Câu hỏi: Cho hai dao động điều hòa củng phương, cùng tần số, cùng biên độ có li độ phụ thuộc thời gian được biểu diễn như hình vẽ, biết $\mathrm{t}_{2}-\mathrm{t}_{1}=\dfrac{1}{20}(\mathrm{~s})$. Một vật có khối lượng 500 g dao động điều hòa có phương trình dao động là tổng hợp của hai dao động điều hòa nói trên. Chọn gốc thế năng ở vị trí cân bằng, lấy $\pi^{2}=10$. Vào thời điểm vật có li độ bằng nửa biên độ thì động năng của vật là

A. $0,4 \mathrm{~J}$.
B. $0,6 \mathrm{~J}$.
C. $0,3 \mathrm{~J}$.
D. $1,2~\text{J}$.
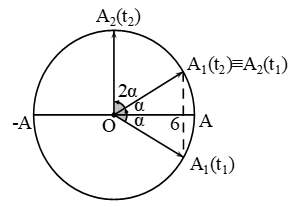
$\alpha +2\alpha =\dfrac{\pi }{2}\Rightarrow \alpha =\dfrac{\pi }{6}\to \Delta \varphi =2\alpha =\dfrac{\pi }{3}$
$A=\dfrac{x}{\cos \alpha }=\dfrac{6}{\cos \left( \pi /6 \right)}=4\sqrt{3}$ (cm)
$A=\sqrt{A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos \Delta \varphi }=\sqrt{2{{\left( 4\sqrt{3} \right)}^{2}}+2{{\left( 4\sqrt{3} \right)}^{2}}\cos \dfrac{\pi }{3}}=12$
$\omega =\dfrac{\Delta \varphi }{{{t}_{2}}-{{t}_{1}}}=\dfrac{\pi /3}{1/20}=\dfrac{20\pi }{3}$
$v=\omega \sqrt{{{A}^{2}}-{{x}^{2}}}=\dfrac{20\pi }{3}\sqrt{{{12}^{2}}-{{6}^{2}}}=40\pi \sqrt{3}(cm/s)=0,4\pi \sqrt{3}(m/s)$
${{W}_{d}}=\dfrac{1}{2}m{{v}^{2}}=\dfrac{1}{2}.0,5.{{\left( 0,4\pi \sqrt{3} \right)}^{2}}\approx 1,2$ (J).

A. $0,4 \mathrm{~J}$.
B. $0,6 \mathrm{~J}$.
C. $0,3 \mathrm{~J}$.
D. $1,2~\text{J}$.
$\alpha +2\alpha =\dfrac{\pi }{2}\Rightarrow \alpha =\dfrac{\pi }{6}\to \Delta \varphi =2\alpha =\dfrac{\pi }{3}$
$A=\dfrac{x}{\cos \alpha }=\dfrac{6}{\cos \left( \pi /6 \right)}=4\sqrt{3}$ (cm)
$A=\sqrt{A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos \Delta \varphi }=\sqrt{2{{\left( 4\sqrt{3} \right)}^{2}}+2{{\left( 4\sqrt{3} \right)}^{2}}\cos \dfrac{\pi }{3}}=12$
$\omega =\dfrac{\Delta \varphi }{{{t}_{2}}-{{t}_{1}}}=\dfrac{\pi /3}{1/20}=\dfrac{20\pi }{3}$
$v=\omega \sqrt{{{A}^{2}}-{{x}^{2}}}=\dfrac{20\pi }{3}\sqrt{{{12}^{2}}-{{6}^{2}}}=40\pi \sqrt{3}(cm/s)=0,4\pi \sqrt{3}(m/s)$
${{W}_{d}}=\dfrac{1}{2}m{{v}^{2}}=\dfrac{1}{2}.0,5.{{\left( 0,4\pi \sqrt{3} \right)}^{2}}\approx 1,2$ (J).
Đáp án D.