Câu hỏi: Cho hình chóp tam giác đều S. ABC cạnh đáy bằng a, đường cao SO = 2a. Gọi M là điểm thuộc đường cao AA1 của tam giác ABC. Xét mặt phẳng (P) đi qua M và vuông góc với AA1. Đặt AM = x.
a) Xác định thiết diện của hình chóp khi cắt bởi mp(P).
b) Tính diện tích thiết diện vừa xác định theo a và x. Xác định vị trí điểm M để diện tích thiết diện đó đạt giá trị lớn nhất.
a) Xác định thiết diện của hình chóp khi cắt bởi mp(P).
b) Tính diện tích thiết diện vừa xác định theo a và x. Xác định vị trí điểm M để diện tích thiết diện đó đạt giá trị lớn nhất.
Lời giải chi tiết
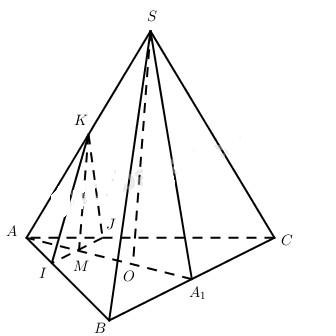
A) Vì
Trường hợp x = 0, thiết diện là điểm A.
Trường hợp
Vậy thiết diện của hình chóp S. ABC khi cắt bởi (P) là tam giác IKJ. Dễ thấy IKJ là tam giác cân tại K.
Trường hợp
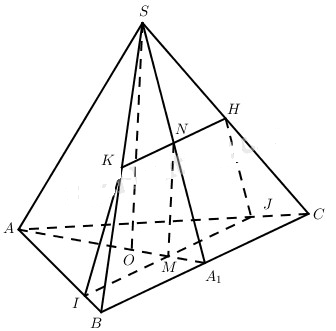
Vậy thiết diện thu được là hình thang IJHK.
Mặt khác M, N lần lượt là trung điểm của IJ, HK; MN // SO;
Trường hợp
b) Trường hợp
Vậy
Trường hợp
Ta có:
Vậy
Dễ thấy khi
Khi
Từ đó, suy ra diện tích thiết diện lớn nhất khi và chỉ khi
Lúc đó diện tích thiết diện bằng
Vậy khi M thay đổi trên AA1 thì diện tích thiết diện lớn nhất bằng
A) Vì
Trường hợp x = 0, thiết diện là điểm A.
Trường hợp
Vậy thiết diện của hình chóp S. ABC khi cắt bởi (P) là tam giác IKJ. Dễ thấy IKJ là tam giác cân tại K.
Trường hợp
Vậy thiết diện thu được là hình thang IJHK.
Mặt khác M, N lần lượt là trung điểm của IJ, HK; MN // SO;
Trường hợp
b) Trường hợp
Vậy
Trường hợp
Ta có:
Vậy
Dễ thấy khi
Khi
Từ đó, suy ra diện tích thiết diện lớn nhất khi và chỉ khi
Lúc đó diện tích thiết diện bằng
Vậy khi M thay đổi trên AA1 thì diện tích thiết diện lớn nhất bằng