Google
Câu hỏi: Cho tam giác ABC vuông tại B. Lấy điểm D bất kì trên đường thẳng vuông góc với mặt phẳng (ABC) kẻ từ điểm A \((S ≢ A)\). Gọi B1, C1 lần lượt là hình chiếu của điểm A trên SB và SC. Chứng minh rằng khi điểm S thay đổi thì
a) Giao tuyến của mặt phẳng (ABC) và mặt phẳng (AB1C1) là đường thẳng cố định và là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
b) Đường thẳng B1C1 đi qua điểm cố định I và \(\widehat {IAB} = \widehat {IC{\rm{A}}}\).
a) Giao tuyến của mặt phẳng (ABC) và mặt phẳng (AB1C1) là đường thẳng cố định và là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
b) Đường thẳng B1C1 đi qua điểm cố định I và \(\widehat {IAB} = \widehat {IC{\rm{A}}}\).
Lời giải chi tiết
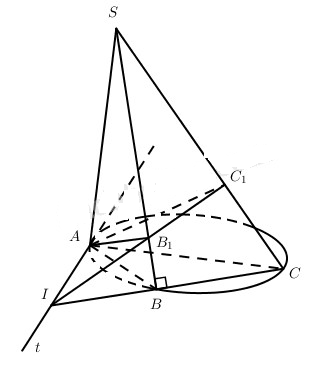
A) Dễ chứng minh được \(SC \bot \left( {A{B_1}{C_1}} \right)\). Gọi At là giao tuyến của (ABC) và (AB1C1) thì \(At \bot SC\). Mặt khác \(SA \bot \left( {ABC} \right)\) nên \(At \bot AC\). Vậy đường thẳng At là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
b) Kí hiệu I là giao điểm của At và đường thẳng BC thì I là điểm có định, mặt khác các điểm I, B1, C1 thuộc cả hai mặt phẳng (AB1C1) và (SBC), do đó các điểm I, B1, C1 thẳng hàng, tức là đường thẳng B1C1 đi qua điểm cố định I khi S thay đổi trên đường thẳng kẻ từ A vuông góc với mp(ABC).
Cũng từ chứng minh trên ta có \(\widehat {IAB} = \widehat {IC{\rm{A}}}\) (cùng chắn cung AB của đường tròn ngoại tiếp tam giác ABC).
A) Dễ chứng minh được \(SC \bot \left( {A{B_1}{C_1}} \right)\). Gọi At là giao tuyến của (ABC) và (AB1C1) thì \(At \bot SC\). Mặt khác \(SA \bot \left( {ABC} \right)\) nên \(At \bot AC\). Vậy đường thẳng At là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
b) Kí hiệu I là giao điểm của At và đường thẳng BC thì I là điểm có định, mặt khác các điểm I, B1, C1 thuộc cả hai mặt phẳng (AB1C1) và (SBC), do đó các điểm I, B1, C1 thẳng hàng, tức là đường thẳng B1C1 đi qua điểm cố định I khi S thay đổi trên đường thẳng kẻ từ A vuông góc với mp(ABC).
Cũng từ chứng minh trên ta có \(\widehat {IAB} = \widehat {IC{\rm{A}}}\) (cùng chắn cung AB của đường tròn ngoại tiếp tam giác ABC).