Câu hỏi: Xác định tâm và bán kính của mặt cầu ngoại tiếp hình chóp \(S. ABC\), biết \(SA = SB = SC = a\), \(\widehat {ASB} = {60^0},\widehat {BSC} = {90^0},\widehat {CSA} = {120^0}\)
Phương pháp giải
- Chứng minh tam giác ABC vuông tại B.
- Từ đó suy ra SH là trục đường tròn ngoại tiếp tam giác ABC (đường thẳng vuông góc với mặt phẳng (ABC) tại tâm đường tròn ngoại tiếp tam giác)
- Sử dụng tính chất: "Mọi điểm nằm trên trục đường tròn ngoại tiếp tam giác ABC thì cách đều ba điểm A, B, C" để dựng tâm mặt cầu.
Lời giải chi tiết
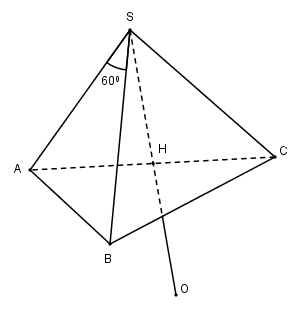
Áp dụng định lí Cosin trong tam giác \(SAB, SAC\) ta có:
\(\eqalign{
& A{B^2} = S{A^2} + S{B^2} - 2SA. SB.\cos {60^0} \cr
& = {a^2} + {a^2} - 2{a^2}.{1 \over 2} = {a^2} \Rightarrow AB = a \cr
& A{C^2} = S{A^2} + S{C^2} - 2SA. SC.\cos {120^0} \cr
& = {a^2} + {a^2} - 2{a^2}\left({ - {1 \over 2}} \right) = 3{a^2}\cr & \Rightarrow AC = a\sqrt 3 \cr} \)
Trong tam giác vuông \(SBC\) có: \(B{C^2} = S{B^2} + S{C^2} = 2{a^2} \) \(\Rightarrow BC = a\sqrt 2 \)
Ta có: \(A{C^2} = A{B^2} + B{C^2} \Rightarrow \Delta ABC\) vuông tại \(B\).
Gọi \(H\) là trung điểm của \(AC\) thì \(H\) là tâm đường tròn ngoại tiếp tam giác ABC.
Vì \(SA = SB = SC\) nên \(SH \bot mp\left( {ABC} \right)\)
Và \(S{H^2} = S{C^2} - H{C^2} \) \(= {a^2} - {\left( {{{a\sqrt 3 } \over 2}} \right)^2}\) \(= {{{a^2}} \over 4} \Rightarrow SH = {a \over 2}\)
Gọi O là điểm đối xứng của S qua H.
Khi đó \(OS = 2SH = 2.\frac{a}{2} = a\).
Tam giác OAH vuông tại \(H\) nên theo Pitago ta có
\(OA = \sqrt {A{H^2} + O{H^2}} \) \(= \sqrt {{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left({\frac{a}{2}} \right)}^2}} = a\)
Lại có SH là trục đường tròn ngoại tiếp tam giác ABC và \(O \in SH\) nên \(OA = OB = OC = a\).
Vậy \(OS = OA = OB = OC = a\) hay \(O\) là tâm mặt cầu ngoại tiếp hình chóp \(S. ABC\) và bán kính \(R = a\).
Cách khác:
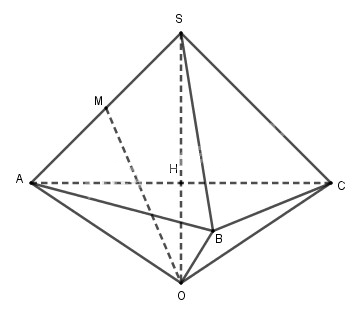
Ta có: \(HA = HB = HC\), \(SA = SB = SC\) nên \(SH\) là trục đường tròn ngoại tiếp tam giác ABC
\(\Rightarrow \) tâm mặt cầu ngoại tiếp hình chóp S. ABC nằm trên \(SH\).
Gọi M là trung điểm của SA.
Trong \(\left( {SAC} \right)\), kẻ đường thẳng \(d\) đi qua M và vuông góc \(SA\) cắt \(SH\) tại \(O\)
(\(d\) là đường trung trực của \(SA\) )
Khi đó:
\(O \in SH \Rightarrow OA = OB = OC\)
\(O \in d \Rightarrow OS = OA\)
\(\Rightarrow \) \(OS = OA = OB = OC\) hay O là tâm mặt cầu ngoại tiếp hình chóp S. ABC.
Xét \(\Delta SMO\) và \(\Delta SHA\) có:
\(\widehat S\) chung
\(\widehat {SMO} = \widehat {SHA} = {90^0}\)
\(\begin{array}{l} \Rightarrow \Delta SMO \sim \Delta SHA\left( {g - g} \right)\\ \Rightarrow \frac{{SM}}{{SH}} = \frac{{SO}}{{SA}} \Rightarrow SM. SA = SH. SO\\ \Rightarrow \frac{1}{2}SA. SA = SH. SO\\ \Rightarrow \frac{1}{2}{a^2} = \frac{a}{2}. SO \Rightarrow SO = a\end{array}\)
Vậy bán kính \(R = a\).
- Chứng minh tam giác ABC vuông tại B.
- Từ đó suy ra SH là trục đường tròn ngoại tiếp tam giác ABC (đường thẳng vuông góc với mặt phẳng (ABC) tại tâm đường tròn ngoại tiếp tam giác)
- Sử dụng tính chất: "Mọi điểm nằm trên trục đường tròn ngoại tiếp tam giác ABC thì cách đều ba điểm A, B, C" để dựng tâm mặt cầu.
Lời giải chi tiết
Áp dụng định lí Cosin trong tam giác \(SAB, SAC\) ta có:
\(\eqalign{
& A{B^2} = S{A^2} + S{B^2} - 2SA. SB.\cos {60^0} \cr
& = {a^2} + {a^2} - 2{a^2}.{1 \over 2} = {a^2} \Rightarrow AB = a \cr
& A{C^2} = S{A^2} + S{C^2} - 2SA. SC.\cos {120^0} \cr
& = {a^2} + {a^2} - 2{a^2}\left({ - {1 \over 2}} \right) = 3{a^2}\cr & \Rightarrow AC = a\sqrt 3 \cr} \)
Trong tam giác vuông \(SBC\) có: \(B{C^2} = S{B^2} + S{C^2} = 2{a^2} \) \(\Rightarrow BC = a\sqrt 2 \)
Ta có: \(A{C^2} = A{B^2} + B{C^2} \Rightarrow \Delta ABC\) vuông tại \(B\).
Gọi \(H\) là trung điểm của \(AC\) thì \(H\) là tâm đường tròn ngoại tiếp tam giác ABC.
Vì \(SA = SB = SC\) nên \(SH \bot mp\left( {ABC} \right)\)
Và \(S{H^2} = S{C^2} - H{C^2} \) \(= {a^2} - {\left( {{{a\sqrt 3 } \over 2}} \right)^2}\) \(= {{{a^2}} \over 4} \Rightarrow SH = {a \over 2}\)
Gọi O là điểm đối xứng của S qua H.
Khi đó \(OS = 2SH = 2.\frac{a}{2} = a\).
Tam giác OAH vuông tại \(H\) nên theo Pitago ta có
\(OA = \sqrt {A{H^2} + O{H^2}} \) \(= \sqrt {{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left({\frac{a}{2}} \right)}^2}} = a\)
Lại có SH là trục đường tròn ngoại tiếp tam giác ABC và \(O \in SH\) nên \(OA = OB = OC = a\).
Vậy \(OS = OA = OB = OC = a\) hay \(O\) là tâm mặt cầu ngoại tiếp hình chóp \(S. ABC\) và bán kính \(R = a\).
Cách khác:
Ta có: \(HA = HB = HC\), \(SA = SB = SC\) nên \(SH\) là trục đường tròn ngoại tiếp tam giác ABC
\(\Rightarrow \) tâm mặt cầu ngoại tiếp hình chóp S. ABC nằm trên \(SH\).
Gọi M là trung điểm của SA.
Trong \(\left( {SAC} \right)\), kẻ đường thẳng \(d\) đi qua M và vuông góc \(SA\) cắt \(SH\) tại \(O\)
(\(d\) là đường trung trực của \(SA\) )
Khi đó:
\(O \in SH \Rightarrow OA = OB = OC\)
\(O \in d \Rightarrow OS = OA\)
\(\Rightarrow \) \(OS = OA = OB = OC\) hay O là tâm mặt cầu ngoại tiếp hình chóp S. ABC.
Xét \(\Delta SMO\) và \(\Delta SHA\) có:
\(\widehat S\) chung
\(\widehat {SMO} = \widehat {SHA} = {90^0}\)
\(\begin{array}{l} \Rightarrow \Delta SMO \sim \Delta SHA\left( {g - g} \right)\\ \Rightarrow \frac{{SM}}{{SH}} = \frac{{SO}}{{SA}} \Rightarrow SM. SA = SH. SO\\ \Rightarrow \frac{1}{2}SA. SA = SH. SO\\ \Rightarrow \frac{1}{2}{a^2} = \frac{a}{2}. SO \Rightarrow SO = a\end{array}\)
Vậy bán kính \(R = a\).