Câu hỏi: Cho tứ diện \(ABCD\). Gọi \(M\), \(N\), \(P\), \(Q\), \(R\) và \(S\) lần lượt trung điểm của \(AB, CD, BC, AD, AC\) và \(BD\). Chứng minh rằng tứ giác \(MPNQ\) là hình bình hành. Từ đó suy ra ba đoạn thẳng \(MN, PQ\) và \(RS\) cắt nhau tại trung điểm mỗi đoạn.
Phương pháp giải
Sử dụng định lý đường trung bình của tam giác.
Sử dụng tính chất hai đường chéo của hình bình hành cắt nhau tại trung điểm mỗi đường.
Lời giải chi tiết
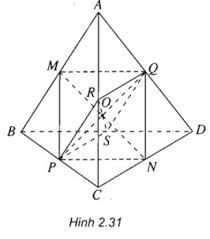
Trong tam giác \(ABC\) ta có: \(MP\parallel AC\) và \(MP = \dfrac{AC}{2}\).
Trong tam giác \(ACD\) ta có: \(QN \parallel AC\) và \(QN = \dfrac{AC}{2}\).
Từ đó suy ra \(\left\{ \begin{array}{l}MP\parallel QN\\ MP = QN\end{array} \right.\)
⇒ Tứ giác \(MPNQ\) là hình bình hành.
Do vậy hai đường chéo \(MN\) và \(PQ\) cắt nhau tại trung điểm \(O \) của mỗi đường.
Tương tự: \(PR \parallel QS\) và \(PR = QS = \dfrac{AB}{2}\).
Do đó tứ giác \(PRQS\) là hình bình hành.
Suy ra hai đường chéo \(PQ\) và \(RS\) cắt nhau tại trung điểm \(O\) của \(PQ\) và \(OR = OS\)
Vậy ba đoạn thẳng \(MN, PQ\) và \(RS\) cắt nhau tại trung điểm mỗi đoạn.
Sử dụng định lý đường trung bình của tam giác.
Sử dụng tính chất hai đường chéo của hình bình hành cắt nhau tại trung điểm mỗi đường.
Lời giải chi tiết
Trong tam giác \(ABC\) ta có: \(MP\parallel AC\) và \(MP = \dfrac{AC}{2}\).
Trong tam giác \(ACD\) ta có: \(QN \parallel AC\) và \(QN = \dfrac{AC}{2}\).
Từ đó suy ra \(\left\{ \begin{array}{l}MP\parallel QN\\ MP = QN\end{array} \right.\)
⇒ Tứ giác \(MPNQ\) là hình bình hành.
Do vậy hai đường chéo \(MN\) và \(PQ\) cắt nhau tại trung điểm \(O \) của mỗi đường.
Tương tự: \(PR \parallel QS\) và \(PR = QS = \dfrac{AB}{2}\).
Do đó tứ giác \(PRQS\) là hình bình hành.
Suy ra hai đường chéo \(PQ\) và \(RS\) cắt nhau tại trung điểm \(O\) của \(PQ\) và \(OR = OS\)
Vậy ba đoạn thẳng \(MN, PQ\) và \(RS\) cắt nhau tại trung điểm mỗi đoạn.