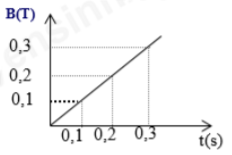
Câu hỏi: Vòng dây kim loại diện tích S, hợp với vectơ cảm ứng từ một góc ${30\circ}$, cho biết độ lớn của cảm ứng từ biến thiên theo thời gian như đồ thị, suất điện động cảm ứng sinh ra có giá trị là:
A. ${0({~V})}$
B. ${\dfrac{S}{2}({~V})}$
C. ${\dfrac{\sqrt{3}}{2}({~V})}$
D. ${S(V)}$

A. ${0({~V})}$
B. ${\dfrac{S}{2}({~V})}$
C. ${\dfrac{\sqrt{3}}{2}({~V})}$
D. ${S(V)}$
Phương pháp:
Công thức tính từ thông: ${\Phi={BS} \cos \alpha}$
Suất điện động cảm ứng: ${{e}_{{c}}=-\dfrac{{d} \Phi}{{dt}}}$
Cách giải:
Từ đồ thị, ta có ${{B}={t}}$
Vòng dây kim loại diện tích S, hợp với vectơ cảm ứng từ một góc ${{30}^{0}}$
${\Rightarrow}$ Góc giữa véctơ cảm ứng từ và véctơ pháp tuyến của vòng dây là $\alpha ={{60}^{0}}$
Công thức tính từ thông: $\Phi =BS.\cos \alpha =t.S.\cos \alpha $
Suất điện động cảm ứng: ${{e}_{c}}=-\dfrac{d\Phi }{dt}=S.\cos \alpha .\dfrac{dB}{dt}=S.\cos \alpha .\dfrac{dt}{dt}=S.\cos {{60}^{0}}=\dfrac{S}{2}$
Công thức tính từ thông: ${\Phi={BS} \cos \alpha}$
Suất điện động cảm ứng: ${{e}_{{c}}=-\dfrac{{d} \Phi}{{dt}}}$
Cách giải:
Từ đồ thị, ta có ${{B}={t}}$
Vòng dây kim loại diện tích S, hợp với vectơ cảm ứng từ một góc ${{30}^{0}}$
${\Rightarrow}$ Góc giữa véctơ cảm ứng từ và véctơ pháp tuyến của vòng dây là $\alpha ={{60}^{0}}$
Công thức tính từ thông: $\Phi =BS.\cos \alpha =t.S.\cos \alpha $
Suất điện động cảm ứng: ${{e}_{c}}=-\dfrac{d\Phi }{dt}=S.\cos \alpha .\dfrac{dB}{dt}=S.\cos \alpha .\dfrac{dt}{dt}=S.\cos {{60}^{0}}=\dfrac{S}{2}$
Đáp án B.