Google
Câu hỏi: Trong một thí nghiệm về giao thoa sóng nước, hai nguồn sóng kết hợp $O_1$ và $O_2$ dao động cùng pha, cùng biên độ. Chọn hệ tọa độ vuông góc xOy (thuộc mặt nước) với gốc tọa độ là vị trí đặt nguồn $O_1$ còn nguồn $O_2$ nằm trên trục Oy. Hai điểm P và Q nằm trên Ox có OP = 4,5 cm và OQ = 8 m. Dịch chuyển nguồn $O_2$ trên trục Oy đến vị trí sao cho góc $\widehat{\mathrm{PO}_2 Q}$ có giá trị lớn nhất thì phần tử nước tại P không dao động còn phần tử nước tại Q dao động với biên độ cực đại. Biết giữa P và Q không còn cực đại nào khác. Trên đoạn OP, điểm gần P nhất mà các phần tử nước dao động với biên độ cực đại cách P một đoạn là
A. 2,5 cm.
B. 1,1 cm.
C. 2,0 cm.
D. 3,4 cm.
A. 2,5 cm.
B. 1,1 cm.
C. 2,0 cm.
D. 3,4 cm.
Phương pháp:
Công thức lượng giác: $\tan (a-b)=\dfrac{\tan a-\tan b}{1+\tan a\cdot \tan b}$
Bất đẳng thức Cô – si: $a+b\ge 2\sqrt{ab}$ (dấu “=” xảy ra ⇔ a = b)
Điều kiện cực đại giao thoa: ${{d}_{2}}-{{d}_{1}}=k\lambda $
Điều kiện cực tiểu giao thoa: ${{d}_{2}}-{{d}_{1}}=\left( k+\dfrac{1}{2} \right)\lambda $
Cách giải:
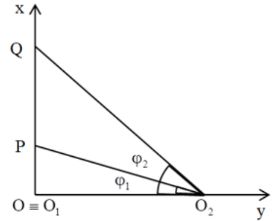Ta có: $P{{O}_{2}}Q={{\varphi }_{2}}-{{\varphi }_{1}}$
$\Rightarrow \tan P{{O}_{2}}Q=\tan \left( {{\varphi }_{2}}-{{\varphi }_{1}} \right)=\dfrac{\tan {{\varphi }_{2}}-\tan {{\varphi }_{1}}}{1+\tan {{\varphi }_{2}}\cdot \tan {{\varphi }_{1}}}$
$\Rightarrow \tan \left( {{\varphi }_{2}}-{{\varphi }_{1}} \right)=\dfrac{\dfrac{{{O}_{1}}Q}{{{O}_{1}}{{O}_{2}}}-\dfrac{{{O}_{1}}P}{{{O}_{1}}{{O}_{2}}}}{1+\dfrac{{{O}_{1}}Q}{{{O}_{1}}{{O}_{2}}}\cdot \dfrac{{{O}_{1}}P}{{{O}_{1}}{{O}_{2}}}}=\dfrac{\dfrac{{{O}_{1}}Q}{a}-\dfrac{{{O}_{1}}P}{a}}{1+\dfrac{{{O}_{1}}Q}{a}\cdot \dfrac{{{O}_{1}}P}{a}}$
$\Rightarrow \tan \left( {{\varphi }_{2}}-{{\varphi }_{1}} \right)=\dfrac{{{O}_{1}}Q-{{O}_{1}}P}{a+\dfrac{{{O}_{1}}Q.{{O}_{1}}P}{a}}=\dfrac{PQ}{a+\dfrac{{{O}_{1}}Q.{{O}_{1}}P}{a}}$
Để $\tan {{\left( {{\varphi }_{2}}-{{\varphi }_{1}} \right)}_{\max }}\Leftrightarrow {{\left( a+\dfrac{{{O}_{1}}Q.{{O}_{1}}P}{a} \right)}_{\min }}$
Áp dụng bất đẳng thức Cô – si, ta có:
$a+\dfrac{{{O}_{1}}Q\cdot {{O}_{1}}P}{a}\ge 2\sqrt{a\cdot \dfrac{{{O}_{1}}Q\cdot {{O}_{1}}P}{a}}$
$\Rightarrow {{\left( a+\dfrac{{{O}_{1}}Q\cdot {{O}_{1}}P}{a} \right)}_{\min }}=2\sqrt{{{O}_{1}}Q\cdot {{O}_{1}}P}$
(Dấu “=” xảy ra $\Leftrightarrow a=\sqrt{{{O}_{1}}Q.{{O}_{1}}P}=\sqrt{4,5.8}=6(\text{cm})$ )
Ta có: ${{O}_{2}}P=\sqrt{{{a}^{2}}+{{O}_{1}}{{P}^{2}}}=\sqrt{{{6}^{2}}+4,{{5}^{2}}}=7,5(\text{cm})$
Lại có: ${{O}_{2}}Q=\sqrt{{{a}^{2}}+{{O}_{1}}{{Q}^{2}}}=\sqrt{{{6}^{2}}+{{8}^{2}}}=10(\text{cm})$
Điểm P không dao động, ta có: $P{{O}_{2}}-P{{O}_{1}}=7,5-4,5=\left( k+\dfrac{1}{2} \right)\lambda $
Điểm Q dao động với biên độ cực đại: $Q{{O}_{2}}-Q{{O}_{1}}=10-8=k\lambda $
Ta có hệ phương trình:
$\left\{ \begin{array}{*{35}{l}}
3=(k+\dfrac{1}{2})\lambda \\
2=k\lambda \\
\end{array}\Rightarrow \left\{ \begin{array}{*{35}{l}}
k=1 \\
\lambda =2(\text{cm}) \\
\end{array} \right. \right.$
→ Q là cực đại bậc 1, giữa P và Q không có cực đại nào khác.
Trên OP, gọi N là điểm gần nhất dao động với biên độ cực đại → N là cực đại bậc 2 ứng với k = 2, ta có: $\sqrt{O{{N}^{2}}+{{a}^{2}}}-ON=2\lambda $
$\Rightarrow \sqrt{O{{N}^{2}}+{{6}^{2}}}-ON=2.2\Rightarrow ON=2,5(\text{cm})$
$\Rightarrow PN={{O}_{1}}P-ON=4,5-2,5=2(\text{cm})$
Công thức lượng giác: $\tan (a-b)=\dfrac{\tan a-\tan b}{1+\tan a\cdot \tan b}$
Bất đẳng thức Cô – si: $a+b\ge 2\sqrt{ab}$ (dấu “=” xảy ra ⇔ a = b)
Điều kiện cực đại giao thoa: ${{d}_{2}}-{{d}_{1}}=k\lambda $
Điều kiện cực tiểu giao thoa: ${{d}_{2}}-{{d}_{1}}=\left( k+\dfrac{1}{2} \right)\lambda $
Cách giải:
$\Rightarrow \tan P{{O}_{2}}Q=\tan \left( {{\varphi }_{2}}-{{\varphi }_{1}} \right)=\dfrac{\tan {{\varphi }_{2}}-\tan {{\varphi }_{1}}}{1+\tan {{\varphi }_{2}}\cdot \tan {{\varphi }_{1}}}$
$\Rightarrow \tan \left( {{\varphi }_{2}}-{{\varphi }_{1}} \right)=\dfrac{\dfrac{{{O}_{1}}Q}{{{O}_{1}}{{O}_{2}}}-\dfrac{{{O}_{1}}P}{{{O}_{1}}{{O}_{2}}}}{1+\dfrac{{{O}_{1}}Q}{{{O}_{1}}{{O}_{2}}}\cdot \dfrac{{{O}_{1}}P}{{{O}_{1}}{{O}_{2}}}}=\dfrac{\dfrac{{{O}_{1}}Q}{a}-\dfrac{{{O}_{1}}P}{a}}{1+\dfrac{{{O}_{1}}Q}{a}\cdot \dfrac{{{O}_{1}}P}{a}}$
$\Rightarrow \tan \left( {{\varphi }_{2}}-{{\varphi }_{1}} \right)=\dfrac{{{O}_{1}}Q-{{O}_{1}}P}{a+\dfrac{{{O}_{1}}Q.{{O}_{1}}P}{a}}=\dfrac{PQ}{a+\dfrac{{{O}_{1}}Q.{{O}_{1}}P}{a}}$
Để $\tan {{\left( {{\varphi }_{2}}-{{\varphi }_{1}} \right)}_{\max }}\Leftrightarrow {{\left( a+\dfrac{{{O}_{1}}Q.{{O}_{1}}P}{a} \right)}_{\min }}$
Áp dụng bất đẳng thức Cô – si, ta có:
$a+\dfrac{{{O}_{1}}Q\cdot {{O}_{1}}P}{a}\ge 2\sqrt{a\cdot \dfrac{{{O}_{1}}Q\cdot {{O}_{1}}P}{a}}$
$\Rightarrow {{\left( a+\dfrac{{{O}_{1}}Q\cdot {{O}_{1}}P}{a} \right)}_{\min }}=2\sqrt{{{O}_{1}}Q\cdot {{O}_{1}}P}$
(Dấu “=” xảy ra $\Leftrightarrow a=\sqrt{{{O}_{1}}Q.{{O}_{1}}P}=\sqrt{4,5.8}=6(\text{cm})$ )
Ta có: ${{O}_{2}}P=\sqrt{{{a}^{2}}+{{O}_{1}}{{P}^{2}}}=\sqrt{{{6}^{2}}+4,{{5}^{2}}}=7,5(\text{cm})$
Lại có: ${{O}_{2}}Q=\sqrt{{{a}^{2}}+{{O}_{1}}{{Q}^{2}}}=\sqrt{{{6}^{2}}+{{8}^{2}}}=10(\text{cm})$
Điểm P không dao động, ta có: $P{{O}_{2}}-P{{O}_{1}}=7,5-4,5=\left( k+\dfrac{1}{2} \right)\lambda $
Điểm Q dao động với biên độ cực đại: $Q{{O}_{2}}-Q{{O}_{1}}=10-8=k\lambda $
Ta có hệ phương trình:
$\left\{ \begin{array}{*{35}{l}}
3=(k+\dfrac{1}{2})\lambda \\
2=k\lambda \\
\end{array}\Rightarrow \left\{ \begin{array}{*{35}{l}}
k=1 \\
\lambda =2(\text{cm}) \\
\end{array} \right. \right.$
→ Q là cực đại bậc 1, giữa P và Q không có cực đại nào khác.
Trên OP, gọi N là điểm gần nhất dao động với biên độ cực đại → N là cực đại bậc 2 ứng với k = 2, ta có: $\sqrt{O{{N}^{2}}+{{a}^{2}}}-ON=2\lambda $
$\Rightarrow \sqrt{O{{N}^{2}}+{{6}^{2}}}-ON=2.2\Rightarrow ON=2,5(\text{cm})$
$\Rightarrow PN={{O}_{1}}P-ON=4,5-2,5=2(\text{cm})$
Đáp án C.