Đây là một bài toán rất hay có thể giải bằng nhiều cách. Một trong số đó là phương pháp giả tưởng tâm quay tức thời và sử dụng khối tâm để giải cho lời giải rất ngắn và đẹp.
Tuy nhiên ở đây, xin giới thiệu cho bạn lời giải bằng kiến thức lớp 10 của một bạn HS :
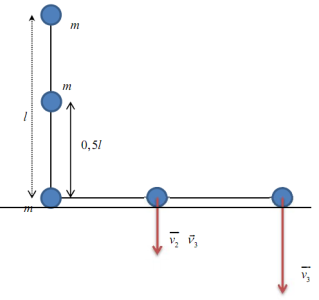
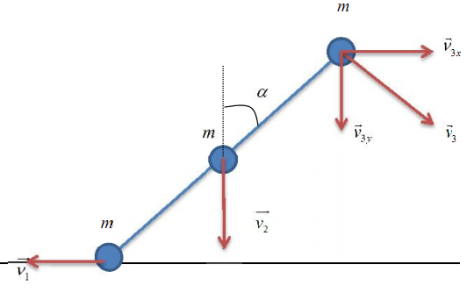
Vì ngoại lực theo phương ngang bằng 0 nên quả cầu giữa chuyển động tịnh tiến đi xuống, quả cầu dưới cùng sang phải. Bảo toàn động lượng $mv_{1}=mv_{3x}\Rightarrow v_{1}=v_{3x}$. (1)
Vì thanh cứng và khoảng cách giữa các quả cầu không thay đổi nên thành phần vận tốc theo phương của thanh bằng nhau: $v_{1}\sin \alpha =v_{2}\cos \alpha =v_{3y}\cos \alpha -v_{3x}\sin \alpha$ (2)
Kết hợp (1) và (2) ta được :
$\begin{cases} &v_{2}=v_{1}\tan \alpha =v_{3x}\tan \alpha \\ &v_{3y}=2v_{1}\tan \alpha =2v_{3x}\tan \alpha \end{cases}$
Định luật bảo toàn cơ năng cho ta:$mg0,5l+mgl=mg0,5l\cos \alpha +mgl\cos \alpha +0,5m\left(v_{1}^2+v_{2}^2+v_{3x}^2+v_{3y}^2\right)$
$\Leftrightarrow 0,5\left(v_{1}^2+v_{2}^2+v_{3x}^2+v_{3y}^2\right)=1,5gl\left(1-\cos \alpha \right)$
Kết hợp các phương trình trên ta được :
$\dfrac{mgl}{2}+mgl=\dfrac{mgl\cos \alpha }{2}+mgl\cos \alpha +\dfrac{m\left(v_{1}^{2}+v_{2}^{2}+v_{3x}^{2}+v_{3y}^{2} \right)}{2}$
$\Leftrightarrow 0,5v_{3x}^2\left(2+5\tan ^2\alpha \right)=1,5gl\left(1-\cos \alpha \right)$
$\Leftrightarrow v_{3x}^2=\dfrac{3gl\left(1-\cos \alpha \right)}{2+5\tan ^2\alpha }$
Lại có :
$v_{3}^2=v_{3x}^2+v_{3y}^2=v_{3x}^2+4v_{3x}^2\tan ^2\alpha =v_{3x}^2\left(1+4\tan ^2\alpha \right)$
$v_{3}^{2}=\dfrac{3gl\left(1-\cos \alpha \right)}{2+5\tan ^{2}\alpha }+\dfrac{12gl\left(1-\cos \alpha \right)}{5+2\cot ^{2}\alpha }$
Khi quả cầu sắp chạm đất thì alpha =90độ. Từ đó thay vào (3) ta được $v_{3}=2\sqrt{\dfrac{3gl}{5}}$