Câu hỏi: Sóng dọc lan truyền trong một môi trường với bước sóng 15 cm với biên độ không đổi $A=5\sqrt{3}$ cm. Gọi M và N là hai điểm cùng nằm trên một phương truyền sóng mà khi chưa có sóng truyền đến lần lượt cách nguồn các khoảng 20 cm và 30 cm. Khoảng cách xa nhất và gần nhất giữa 2 phần tử môi trường tại M và N có sóng truyền qua là bao nhiêu?
A. Lmax = 25 mm, lmin = 0.
B. Lmax = 25 mm, lmin = 25 mm.
C. Lmax = 25 cm, lmin = 0.
D. Lmax = 250 cm, lmin = 0.
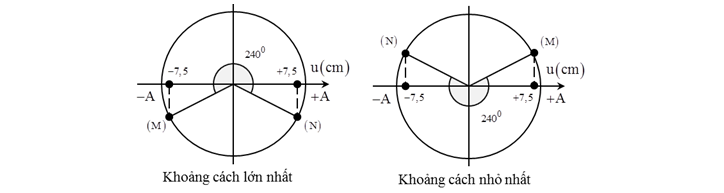
+ Độ lệch pha dao động giữa hai điểm MN: $\Delta \varphi =\dfrac{2\pi \Delta {d}}{\lambda }=\dfrac{2\pi. 10}{15}=\dfrac{4\pi }{3}$
$\Rightarrow $ Khoảng cách giữa hai điểm MN là ${d}=\Delta x+\Delta {{x}_{\varphi }}$, với $\Delta {{x}_{\varphi }}$ là khoảng cách thêm vào do sự dao động dọc theo phương truyền sóng.
+ Từ hình vẽ ta có: ${{l}_{\max }}=25\,\, cm$ (ứng với M chuyển động đến vị trí ${{u}_{M}}=-\dfrac{\sqrt{3}}{2}\, A$ theo chiều dương và N đến vị trí ${{u}_{N}}=+\dfrac{\sqrt{3}}{2}$ A theo chiều dương)
+ ${{l}_{\min }}=0$ (ứng với M chuyển động đến vị trí ${{u}_{M}}=\dfrac{\sqrt{3}}{2}\,\, A$ theo chiều âm và N đến vị trí ${{u}_{N}}=\dfrac{\sqrt{3}}{2}\,\, A$ theo chiều âm)
A. Lmax = 25 mm, lmin = 0.
B. Lmax = 25 mm, lmin = 25 mm.
C. Lmax = 25 cm, lmin = 0.
D. Lmax = 250 cm, lmin = 0.
+ Độ lệch pha dao động giữa hai điểm MN: $\Delta \varphi =\dfrac{2\pi \Delta {d}}{\lambda }=\dfrac{2\pi. 10}{15}=\dfrac{4\pi }{3}$
$\Rightarrow $ Khoảng cách giữa hai điểm MN là ${d}=\Delta x+\Delta {{x}_{\varphi }}$, với $\Delta {{x}_{\varphi }}$ là khoảng cách thêm vào do sự dao động dọc theo phương truyền sóng.
+ Từ hình vẽ ta có: ${{l}_{\max }}=25\,\, cm$ (ứng với M chuyển động đến vị trí ${{u}_{M}}=-\dfrac{\sqrt{3}}{2}\, A$ theo chiều dương và N đến vị trí ${{u}_{N}}=+\dfrac{\sqrt{3}}{2}$ A theo chiều dương)
+ ${{l}_{\min }}=0$ (ứng với M chuyển động đến vị trí ${{u}_{M}}=\dfrac{\sqrt{3}}{2}\,\, A$ theo chiều âm và N đến vị trí ${{u}_{N}}=\dfrac{\sqrt{3}}{2}\,\, A$ theo chiều âm)
Đáp án C.