Câu hỏi: Phả hệ ở hình dưới đây mô tả sự di truyền 2 bệnh ở người, mỗi bệnh đều do một gen có 2 alen quy định; Gen quy định bệnh B nằm ở vùng không tương đồng trên nhiễm sắc thể giới tính X quy định. Biết rằng không xảy ra đột biến. Theo lí thuyết, có bao nhiêu phát biểu sau đây đúng?
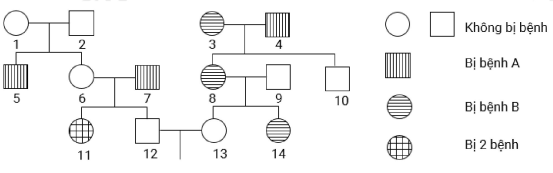
I. Xác định được kiểu gen của 7 người.
II. Xác suất sinh con thứ 3 là con trai bị cả hai bệnh của cặp 8-9 là 12,5%.
III. Xác suất sinh con thứ nhất chỉ bị bệnh B của cặp 12-13 là 5/48.
IV. Xác suất sinh 2 con đều không bị bệnh của cặp 12 - 13 là 5/128.
A. 2.
B. 3
C. 1
D. 4

I. Xác định được kiểu gen của 7 người.
II. Xác suất sinh con thứ 3 là con trai bị cả hai bệnh của cặp 8-9 là 12,5%.
III. Xác suất sinh con thứ nhất chỉ bị bệnh B của cặp 12-13 là 5/48.
IV. Xác suất sinh 2 con đều không bị bệnh của cặp 12 - 13 là 5/128.
A. 2.
B. 3
C. 1
D. 4
Quy ước gen: A: không bị bệnh A, a: bị bệnh A
B: không bị bệnh B, b: Bị bệnh B
Các người xác định được kiểu gen là:
$4\left(Aa{{X}^{B}}Y \right), 6\left(Aa{{X}^{B}}{{X}^{b}} \right), 7\left(Aa{{X}^{B}}Y \right), 8\left(aa{{X}^{B}}{{X}^{b}} \right), 9\left(Aa{{X}^{B}}Y \right), 10\left(Aa{{X}^{B}}Y \right), 11\left(aa{{X}^{b}}{{X}^{b}} \right)$
Người (1), (2) không thể xác định kiểu gen về bệnh A
Ta có:
I đúng.
II đúng. Người số 8 có kiểu gen aa ${{X}^{B}}{{X}^{b}}$ (bị bệnh A và nhận ${{X}^{b}}$ của bố)
Người số 9 có kiểu gen $Aa{{X}^{B}}Y$ (Sinh con bị bênh A và không mắc bệnh B)
1 1Xác suất \sin h con trai bị cả 2 bệnh: = $aa{{X}^{b}}Y=\dfrac{1}{2}aa\times \dfrac{1}{2}{{X}^{B}}\times \dfrac{1}{2}Y=\dfrac{1}{8}$
III đúng. Người số 8 bị bệnh A nên sẽ truyền gen bệnh cho người số 13.
Người số 13 có kiểu gen dị hợp về bệnh A
- Xác suất \sin h con của cặp 12-13:
Người 12 có em gái mắc cả 2 bệnh nên có kiểu gen :(1AA:2Aa)XBY
Người 13 có mẹ mang gen gây bệnh B và bị bệnh A: $\left(aa{{X}^{B}}{{X}^{b}} \right),$ bố $9\left(Aa{{X}^{B}}Y \right)\to $ người 13 có kiểu gen: $Aa\left({{X}^{B}}{{X}^{B}}:{{X}^{B}}{{X}^{b}} \right)$
Cặp 12 – 13: $\left(1AA:2Aa \right){{X}^{B}}Y\times Aa\left({{X}^{B}}{{X}^{B}}:{{X}^{B}}{{X}^{b}} \right)\leftrightarrow \left(2A:1a \right)\left(1{{X}^{B}}:1Y \right)\times \left(1A:1a \right)\left(3{{X}^{B}}:1{{X}^{b}} \right)$
Xác suất học \sin h người con chỉ bị bệnh B là: $A-{{X}^{B}}Y=\left(1-\dfrac{1}{3}a\times \dfrac{1}{2}a \right)\left(\dfrac{1}{2}Y\times \dfrac{1}{4}{{X}^{b}} \right)=\dfrac{5}{48}$
IV sai. Xác suất họ \sin h 2 con không bị bệnh:
+ Sinh 2 con không bị bệnh A: $\dfrac{1}{3}AA+\dfrac{2}{3}Aa\times {{\left(\dfrac{3}{4}A- \right)}^{2}}=\dfrac{17}{24}$ (vì 1/3AA luôn tạo đời con không bị bệnh)
+ Sinh 2 con không bị bệnh B: $\dfrac{1}{2}{{X}^{B}}{{X}^{B}}+\dfrac{1}{2}{{X}^{B}}{{X}^{b}}\times {{\left(\dfrac{3}{4}{{X}^{B}}- \right)}^{2}}=\dfrac{25}{32}$
Vậy tỉ lệ cần tính là: $\dfrac{17}{24}\times \dfrac{25}{32}=\dfrac{425}{768}$
B: không bị bệnh B, b: Bị bệnh B
Các người xác định được kiểu gen là:
$4\left(Aa{{X}^{B}}Y \right), 6\left(Aa{{X}^{B}}{{X}^{b}} \right), 7\left(Aa{{X}^{B}}Y \right), 8\left(aa{{X}^{B}}{{X}^{b}} \right), 9\left(Aa{{X}^{B}}Y \right), 10\left(Aa{{X}^{B}}Y \right), 11\left(aa{{X}^{b}}{{X}^{b}} \right)$
Người (1), (2) không thể xác định kiểu gen về bệnh A
Ta có:
I đúng.
II đúng. Người số 8 có kiểu gen aa ${{X}^{B}}{{X}^{b}}$ (bị bệnh A và nhận ${{X}^{b}}$ của bố)
Người số 9 có kiểu gen $Aa{{X}^{B}}Y$ (Sinh con bị bênh A và không mắc bệnh B)
1 1Xác suất \sin h con trai bị cả 2 bệnh: = $aa{{X}^{b}}Y=\dfrac{1}{2}aa\times \dfrac{1}{2}{{X}^{B}}\times \dfrac{1}{2}Y=\dfrac{1}{8}$
III đúng. Người số 8 bị bệnh A nên sẽ truyền gen bệnh cho người số 13.
Người số 13 có kiểu gen dị hợp về bệnh A
- Xác suất \sin h con của cặp 12-13:
Người 12 có em gái mắc cả 2 bệnh nên có kiểu gen :(1AA:2Aa)XBY
Người 13 có mẹ mang gen gây bệnh B và bị bệnh A: $\left(aa{{X}^{B}}{{X}^{b}} \right),$ bố $9\left(Aa{{X}^{B}}Y \right)\to $ người 13 có kiểu gen: $Aa\left({{X}^{B}}{{X}^{B}}:{{X}^{B}}{{X}^{b}} \right)$
Cặp 12 – 13: $\left(1AA:2Aa \right){{X}^{B}}Y\times Aa\left({{X}^{B}}{{X}^{B}}:{{X}^{B}}{{X}^{b}} \right)\leftrightarrow \left(2A:1a \right)\left(1{{X}^{B}}:1Y \right)\times \left(1A:1a \right)\left(3{{X}^{B}}:1{{X}^{b}} \right)$
Xác suất học \sin h người con chỉ bị bệnh B là: $A-{{X}^{B}}Y=\left(1-\dfrac{1}{3}a\times \dfrac{1}{2}a \right)\left(\dfrac{1}{2}Y\times \dfrac{1}{4}{{X}^{b}} \right)=\dfrac{5}{48}$
IV sai. Xác suất họ \sin h 2 con không bị bệnh:
+ Sinh 2 con không bị bệnh A: $\dfrac{1}{3}AA+\dfrac{2}{3}Aa\times {{\left(\dfrac{3}{4}A- \right)}^{2}}=\dfrac{17}{24}$ (vì 1/3AA luôn tạo đời con không bị bệnh)
+ Sinh 2 con không bị bệnh B: $\dfrac{1}{2}{{X}^{B}}{{X}^{B}}+\dfrac{1}{2}{{X}^{B}}{{X}^{b}}\times {{\left(\dfrac{3}{4}{{X}^{B}}- \right)}^{2}}=\dfrac{25}{32}$
Vậy tỉ lệ cần tính là: $\dfrac{17}{24}\times \dfrac{25}{32}=\dfrac{425}{768}$
Đáp án B.