Câu hỏi: Một vật có khối lượng $400 \mathrm{~g}$ dao động điều hòa. Sự phụ thuộc của thế năng của vật theo thời gian được cho như hình vẽ.
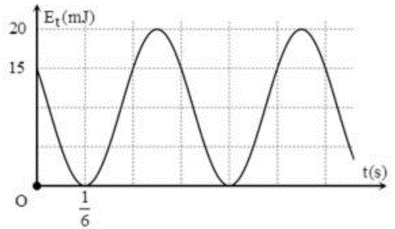
Tại thời điểm $t=0$, vật chuyển động theo chiều dương. Lấy $\pi^{2}=10$. Phương trình dao động của vật là
A. $x=5 \cos \left(2 \pi t-\dfrac{\pi}{3}\right)(\mathrm{cm})$.
B. $\mathrm{x}=10 \cos \left(\pi \mathrm{t}+\dfrac{\pi}{6}\right)(\mathrm{cm})$.
C. $x=5 \cos \left(2 \pi t-\dfrac{5 \pi}{6}\right)(\mathrm{cm})$.
D. $x=10 \cos \left(\pi t-\dfrac{\pi}{6}\right)(\mathrm{cm})$.

Tại thời điểm $t=0$, vật chuyển động theo chiều dương. Lấy $\pi^{2}=10$. Phương trình dao động của vật là
A. $x=5 \cos \left(2 \pi t-\dfrac{\pi}{3}\right)(\mathrm{cm})$.
B. $\mathrm{x}=10 \cos \left(\pi \mathrm{t}+\dfrac{\pi}{6}\right)(\mathrm{cm})$.
C. $x=5 \cos \left(2 \pi t-\dfrac{5 \pi}{6}\right)(\mathrm{cm})$.
D. $x=10 \cos \left(\pi t-\dfrac{\pi}{6}\right)(\mathrm{cm})$.
$\dfrac{T}{2}=3\hat{o}\Rightarrow T=6\hat{o}=6.\dfrac{1}{6}=1s\to \omega =\dfrac{2\pi }{T}=2\pi $ (rad/s)
$E=\dfrac{1}{2}m{{\omega }^{2}}{{A}^{2}}\Rightarrow {{20.10}^{-3}}=\dfrac{1}{2}.0,4.{{\left( 2\pi \right)}^{2}}{{A}^{2}}\Rightarrow A=0,05m=5cm$
$\dfrac{{{E}_{t}}}{E}={{\left( \dfrac{x}{A} \right)}^{2}}=\dfrac{3}{4}\Rightarrow \left| x \right|=\dfrac{A\sqrt{3}}{2}\downarrow $ theo chiều dương $\Rightarrow x=-\dfrac{A\sqrt{3}}{2}$ theo chiều dương $\Rightarrow \varphi ==-\dfrac{5\pi }{6}$
$E=\dfrac{1}{2}m{{\omega }^{2}}{{A}^{2}}\Rightarrow {{20.10}^{-3}}=\dfrac{1}{2}.0,4.{{\left( 2\pi \right)}^{2}}{{A}^{2}}\Rightarrow A=0,05m=5cm$
$\dfrac{{{E}_{t}}}{E}={{\left( \dfrac{x}{A} \right)}^{2}}=\dfrac{3}{4}\Rightarrow \left| x \right|=\dfrac{A\sqrt{3}}{2}\downarrow $ theo chiều dương $\Rightarrow x=-\dfrac{A\sqrt{3}}{2}$ theo chiều dương $\Rightarrow \varphi ==-\dfrac{5\pi }{6}$
Đáp án C.