Câu hỏi: Một học sinh xác định độ tự cảm L của cuộn dây bằng cách đặt điện áp xoay chiều $u=U\sqrt{2}\cos 2\pi ft$ (U không đổi, f thay đổi) vào hai đầu đoạn mạch gồm cuộn dây đó mắc nối tiếpvới điện trở bảo vệ R0. Gọi Z là tổng trở của mạch. Thay đổi f, đọc giá trị f và Z tương ứng. Dựa vào kết quả thực nghiệm học sinh này vẽ được đồ thị ${{Z}^{2}}$ theo ${{f}^{2}}$. Giá trị của độ tự cảm L đo được là
A. 0,447H
B. 0,318H
C. 0,626H
D. 0,159H

A. 0,447H
B. 0,318H
C. 0,626H
D. 0,159H
Phương pháp:
+ Sử dụng kĩ năng đọc đồ thị
+ Sử dụng biểu thức tính tổng trở: $Z=\sqrt{{{R}^{2}}+Z_{L}^{2}}$
Cách giải:
Tổng trở của mạch: $Z=\sqrt{R_{0}^{2}+Z_{L}^{2}}\Rightarrow {{Z}^{2}}=R_{0}^{2}+Z_{L}^{2}=R_{0}^{2}+4{{\pi }^{2}}{{f}^{2}}{{L}^{2}}$
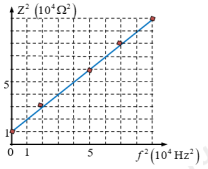
Từ đồ thị, ta có:
+ Khi ${{f}^{2}}=0\Rightarrow {{Z}^{2}}=R_{0}^{2}={{10}^{4}}\Rightarrow {{R}_{0}}=100\Omega $
+ Khi ${{f}^{2}}={{4.10}^{4}}\Rightarrow {{Z}^{2}}={{5.10}^{4}}=R_{0}^{2}+4{{\pi }^{2}}{{f}^{2}}{{L}^{2}}$
$\Rightarrow {{L}^{2}}=\dfrac{{{Z}^{2}}-R_{0}^{2}}{4{{\pi }^{2}}{{f}^{2}}}=\dfrac{{{5.10}^{4}}-{{10}^{4}}}{4{{\pi }^{2}}{{.4.10}^{4}}}=\dfrac{1}{4{{\pi }^{2}}}\Rightarrow L=\dfrac{1}{2\pi }H$
+ Sử dụng kĩ năng đọc đồ thị
+ Sử dụng biểu thức tính tổng trở: $Z=\sqrt{{{R}^{2}}+Z_{L}^{2}}$
Cách giải:
Tổng trở của mạch: $Z=\sqrt{R_{0}^{2}+Z_{L}^{2}}\Rightarrow {{Z}^{2}}=R_{0}^{2}+Z_{L}^{2}=R_{0}^{2}+4{{\pi }^{2}}{{f}^{2}}{{L}^{2}}$
Từ đồ thị, ta có:
+ Khi ${{f}^{2}}=0\Rightarrow {{Z}^{2}}=R_{0}^{2}={{10}^{4}}\Rightarrow {{R}_{0}}=100\Omega $
+ Khi ${{f}^{2}}={{4.10}^{4}}\Rightarrow {{Z}^{2}}={{5.10}^{4}}=R_{0}^{2}+4{{\pi }^{2}}{{f}^{2}}{{L}^{2}}$
$\Rightarrow {{L}^{2}}=\dfrac{{{Z}^{2}}-R_{0}^{2}}{4{{\pi }^{2}}{{f}^{2}}}=\dfrac{{{5.10}^{4}}-{{10}^{4}}}{4{{\pi }^{2}}{{.4.10}^{4}}}=\dfrac{1}{4{{\pi }^{2}}}\Rightarrow L=\dfrac{1}{2\pi }H$
Đáp án D.