Câu hỏi: Một con lắc lò xo treo thẳng đứng. Từ vị trí cân bằng, nâng vật nhỏ của con lắc theo phương thẳng đứng lên đến vị trí lò xo không biến dạng rồi đồng thời truyền cho vật vận tốc $10 \pi \sqrt{3} \dfrac{\mathrm{cm}}{\mathrm{s}}$ hướng về vị trí cân bằng. Con lắc dao động điều hòa với tần số $5 \mathrm{~Hz}$. Lấy $\mathrm{g}=10 \dfrac{\mathrm{m}}{\mathrm{s}^{2}} ; \pi^{2}=10$. Trong một chu kì dao động khoảng thời gian mà lực kéo về và lực đàn hồi của lò xo tác dụng lên vật cùng hướng nhau là
A. $\dfrac{1}{6}$ s.
B. $\dfrac{1}{60} \mathrm{~s}$.
C. $\dfrac{1}{30} \mathrm{~s}$.
D. $\dfrac{1}{12} \mathrm{~s}$.
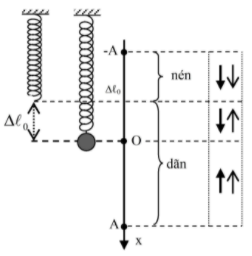
$\omega =2\pi f=2\pi .5=10\pi $ (rad/s)
$\Delta {{l}_{0}}=\dfrac{g}{{{\omega }^{2}}}\approx \dfrac{{{\pi }^{2}}}{{{\left( 10\pi \right)}^{2}}}=0,01m=1cm$
$A=\sqrt{\Delta l_{0}^{2}+{{\left( \dfrac{v}{\omega } \right)}^{2}}}=\sqrt{{{1}^{2}}+{{\left( \dfrac{10\pi \sqrt{3}}{10\pi } \right)}^{2}}}=2$ (cm)
$\Delta t=\dfrac{2\pi -2\arcsin \dfrac{\Delta {{l}_{0}}}{A}}{\omega }=\dfrac{2\pi -2\arcsin \dfrac{1}{2}}{10\pi }=\dfrac{1}{6}$ (s).
A. $\dfrac{1}{6}$ s.
B. $\dfrac{1}{60} \mathrm{~s}$.
C. $\dfrac{1}{30} \mathrm{~s}$.
D. $\dfrac{1}{12} \mathrm{~s}$.
$\omega =2\pi f=2\pi .5=10\pi $ (rad/s)
$\Delta {{l}_{0}}=\dfrac{g}{{{\omega }^{2}}}\approx \dfrac{{{\pi }^{2}}}{{{\left( 10\pi \right)}^{2}}}=0,01m=1cm$
$A=\sqrt{\Delta l_{0}^{2}+{{\left( \dfrac{v}{\omega } \right)}^{2}}}=\sqrt{{{1}^{2}}+{{\left( \dfrac{10\pi \sqrt{3}}{10\pi } \right)}^{2}}}=2$ (cm)
$\Delta t=\dfrac{2\pi -2\arcsin \dfrac{\Delta {{l}_{0}}}{A}}{\omega }=\dfrac{2\pi -2\arcsin \dfrac{1}{2}}{10\pi }=\dfrac{1}{6}$ (s).
Đáp án A.