Câu hỏi: Một chất điểm tham gia đồng thời hai dao động có đồ thị li độ như hình vẽ.
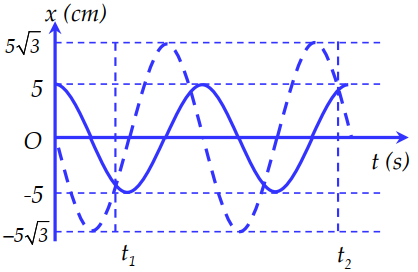
Biết $\mathrm{t}_{2}-\mathrm{t}_{1}=0,3 \mathrm{~s}$. Thời điểm vận tốc v và li độ x của chất điểm thỏa mãn $\mathrm{v}=\omega \mathrm{x}$ lần thứ 2022 kể từ thời điểm ban đầu có giá trị gần nhất với giá trị nào sau đây?
A. 101,1 s.
B. 202,1 s.
C. 104,2 s.
D. $204,2 \mathrm{~s}$.
$x={{x}_{1}}+{{x}_{2}}=5\angle 0+5\sqrt{3}\angle \dfrac{\pi }{2}=10\angle \dfrac{\pi }{3}$
$v=\omega x\Rightarrow \sqrt{{{A}^{2}}-{{x}^{2}}}=\left| x \right|\Rightarrow \left| x \right|=\dfrac{A\sqrt{2}}{2}$ và v cùng dấu x
$t=\dfrac{2020\pi +\dfrac{2\pi }{3}+\dfrac{3\pi }{4}}{10\pi }\approx 202,1s$.

Biết $\mathrm{t}_{2}-\mathrm{t}_{1}=0,3 \mathrm{~s}$. Thời điểm vận tốc v và li độ x của chất điểm thỏa mãn $\mathrm{v}=\omega \mathrm{x}$ lần thứ 2022 kể từ thời điểm ban đầu có giá trị gần nhất với giá trị nào sau đây?
A. 101,1 s.
B. 202,1 s.
C. 104,2 s.
D. $204,2 \mathrm{~s}$.
${{t}_{2}}-{{t}_{1}}=3.\dfrac{T}{2}=0,3\Rightarrow T=0,2s\to \omega =\dfrac{2\pi }{T}=10\pi $ (rad/s)$x={{x}_{1}}+{{x}_{2}}=5\angle 0+5\sqrt{3}\angle \dfrac{\pi }{2}=10\angle \dfrac{\pi }{3}$
$v=\omega x\Rightarrow \sqrt{{{A}^{2}}-{{x}^{2}}}=\left| x \right|\Rightarrow \left| x \right|=\dfrac{A\sqrt{2}}{2}$ và v cùng dấu x
$t=\dfrac{2020\pi +\dfrac{2\pi }{3}+\dfrac{3\pi }{4}}{10\pi }\approx 202,1s$.
Đáp án B.